-
网址:http://m.1010jiajiao.com/paper/timu/5157761.html[举报]
首先必须确定直线与平面平行,然后将直线到平面的距离问题转化成直线上一点到平面的距离问题。
例4、已知边长为
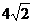 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,求AE与平面α间的距离。
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,求AE与平面α间的距离。 分析:因为AE∥平面α,所以将AE与平面α的距离转化成点A到平面α的距离,建立如图右手直角坐标系,
分析:因为AE∥平面α,所以将AE与平面α的距离转化成点A到平面α的距离,建立如图右手直角坐标系, 则A(0,0,0),P(0,0,2),
 E(
E( ,0,0),F(
,0,0),F( ,
, ,0),
P
,0),
P




 ,
, ,
A F
,
A F
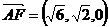 ,设法向量
,设法向量 =(x,y,z), B
E C
=(x,y,z), B
E C则由
 ,
, 得,
得,

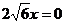
 x=0
x=0
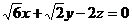
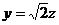 不妨设防z=1,则
不妨设防z=1,则 =(0,
=(0, ,1),所以依公式可得所求距离为
,1),所以依公式可得所求距离为
- 题目来源:高考数学探析法向量在立体几何解题中的应用