-
网址:http://m.1010jiajiao.com/paper/timu/5155932.html[举报]
18.(12分)
已知a、b、m、
 ,
, 是首项为a,公差为b的等差数列;
是首项为a,公差为b的等差数列; 是首项为b,公比为a的等比数列,且满足
是首项为b,公比为a的等比数列,且满足 .
.(1)求a的值;
(2)数列
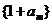 与数列
与数列 的公共项,且公共项按原顺序排列后构成一个新数列
的公共项,且公共项按原顺序排列后构成一个新数列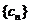 ,求
,求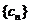 的前n项之和
的前n项之和 .
. - 题目来源:08高考数学冲刺预测卷二 第Ⅰ卷(选择题,共60分)
参考答案
1.C 2.C 3.B 4.D 5.D 6.A 7.B 8.C 9.D 10.(文)B (理)B 11.(文)C (理)C 12.(文)B (理)B
13.[4,6] 14. 15.34.15% 16.
15.34.15% 16.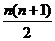
17.由已知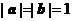 .
.
∵  ,∴
,∴ 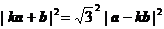 .∴
.∴  .
.
∵ k>0, ∴ 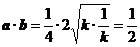 .
.
此时 ∴
∴  . ∴
. ∴  =60°.
=60°.
18.(1)∵  ,
, ,
,
由已知a<b<a+b<ab<a+2b,
∴ 由a+2b<ab,a、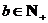 得
得 .
.
∵  , ∴ a≥2.
, ∴ a≥2.
又得 ,而
,而 , ∴ b≥3.
, ∴ b≥3.
再由ab<a+2b,b≥3,得 .
.
∴ 2≤a<3 ∴ a=2.
(2)设 ,即
,即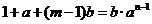 .
.
∴  ,
,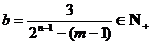 .
.
∵ b≥3, ∴ 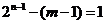 . ∴
. ∴  .∴
.∴ 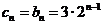 .
.
故 .
.
19.(1)由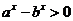 , ∴
, ∴ 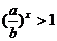 ,
, . ∴ x>0.∴ 定义域为(0,+∞).
. ∴ x>0.∴ 定义域为(0,+∞).
(2)设 , a>1>b>0, ∴
, a>1>b>0, ∴ 


∴  ∴
∴  .
.
∴ 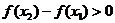 . ∴
. ∴  在(0,+∞)是增函数.
在(0,+∞)是增函数.
(3)当 ,+∞
,+∞ 时,
时,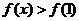 ,要使
,要使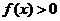 ,须
,须 ,∴ a-b≥1.
,∴ a-b≥1.
20.(1)由P-ABD,Q-CBD是相同正三棱锥,可知△PBD与△QBD是全等等腰△.取BD中点E,连结PE、QE,则BD⊥PE,BD⊥QE.故BD⊥平面PQE,从而BD⊥PQ.
(2)由(1)知∠PEQ是二面角P-BD-Q的平面角,作PM⊥平面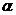 ,垂足为M,作QN⊥平面
,垂足为M,作QN⊥平面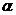 ,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=
,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE= ,PE=QE=
,PE=QE= ,PQ=MN=
,PQ=MN= ,∴cos∠PEQ=
,∴cos∠PEQ=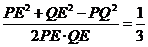 ,即二面角平面角为
,即二面角平面角为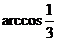 .
.
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则

∴  .
.
∴  .∴
.∴ 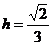 .
.
21.(1)以AB为x轴,以AB中点为原点O建立直角坐标系.
∵  ,
,
∴ 动点轨迹为椭圆,且 ,c=1,从而b=1.
,c=1,从而b=1.
∴ 方程为  .
.
(2)将y=x+t代入 ,得
,得 .
.
设M(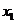 ,
,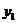 )、N(
)、N(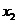 ,
,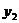 ),
),
∴ 
由①得 <3.
<3.
∴  .
.
∴ t=0时, .
.
22.(理) ,即
,即 ,故x<0或x>1.
,故x<0或x>1.
∴ 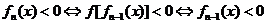 或
或 .
.
要使一切 ,n≥2,都有
,n≥2,都有 ,必须使
,必须使 或
或 ,
,
∴  或
或 ,即
,即 或
或 .
.
解得x<0或x>1或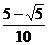
 .
.
∴ 还有区间(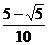 ,
, )和(1,+∞)使得对于这些区间内的任意实数x,只要n≥2,都有
)和(1,+∞)使得对于这些区间内的任意实数x,只要n≥2,都有 .
.
(文)由已知 ,
, .
.
∴  在(-∞,
在(-∞, 上单增,在(2,+∞)上单调.
上单增,在(2,+∞)上单调.
又∵  ,
, .
.
∴ 需讨论 与
与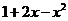 的大小.
的大小.
由 知
知
当 ,即
,即 时,
时, .
.
故 时,应有
时,应有 .
.