-
网址:http://m.1010jiajiao.com/paper/timu/5155696.html[举报]
16、(本小题满分14分)
已知圆C:
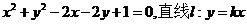 ,且
,且 、
、 两点,点
两点,点
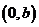 ,且
,且 .
.(1)当

(2)当
 时,求
时,求 的取值范围.
的取值范围. - 题目来源:高三文科数学调研试卷 参考公式: 样本数据,,,的方差 (为样本平均数) 锥体体积公式 柱体体积公式(其中为底面面积、为高) 用最小二乘法求线性回归方程系数公式 ,
江苏省四星级高中通州中学高三数学(文科)调研试卷答案
1、 2、
2、 3、
3、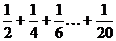 4、
4、 5、
5、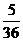 6、40
6、40
7、76 8、3 9、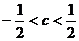 10、
10、 11、
11、 12、
12、
13、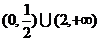 14、②④
14、②④
15、解:(1)设b=(x,y), a.b=-1 有x+y=-1 ①……………………2分
又b与a的夹角为 ,所以a.b=| a||b|π,的以x2+y2=1 ②
,所以a.b=| a||b|π,的以x2+y2=1 ②
由①②解得
故b=(-1,0)或b=(-1,0).…………………………………………7分
(2)由向量b与q垂直知b=(0,-1),由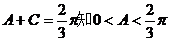 …………9分
…………9分
又因为b+q=
所以|b+q|2=

故当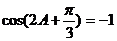 时,|b+p|取得最小值为
时,|b+p|取得最小值为 ………………14分
………………14分
16、解(1)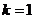 ………………
4分
………………
4分
(2)由 消去y得
消去y得
 ①
①
设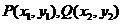 则
则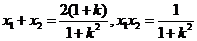 ………………6分
………………6分
 8分
8分
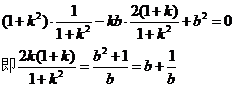
令
当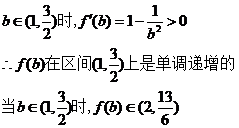 ……………… 11分
……………… 11分
 解得:
解得: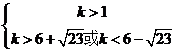
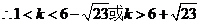 ……………… 13分
……………… 13分
由①式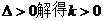
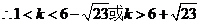
 ……………… 14分
……………… 14分
17、证明:(Ⅰ)∵ ,∴
,∴ .
.
∵三棱柱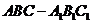 为直三棱柱,∴
为直三棱柱,∴ .
.
∵ ,∴
,∴ 平面
平面 .
.
∵ 平面
平面 ,∴
,∴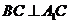 ,
,
∵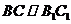 ,则
,则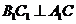 . ……4分
. ……4分
在 中,
中,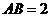 ,
,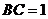 ,∴
,∴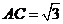 .
.
∵ ,∴四边形
,∴四边形 为正方形.
为正方形.
∴ . ……6分
. ……6分
∵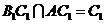 ,∴
,∴
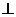 平面
平面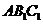 .
……7分
.
……7分
(Ⅱ)当点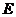 为棱
为棱 的中点时,
的中点时,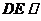 平面
平面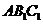 . ……9分
. ……9分
证明如下:
如图,取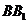 的中点
的中点 ,连
,连 、
、 、
、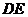 ,
,
∵ 、
、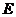 、
、 分别为
分别为 、
、 、
、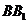 的中点,
的中点,
 ∴
∴ .
.
∵ 平面
平面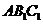 ,
,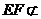 平面
平面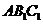 ,
,
∴ 平面
平面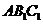 . ……12分
. ……12分
同理可证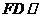 平面
平面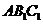 .
.
∵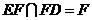 ,
,
∴平面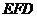
 平面
平面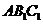 .
.
∵ 平面
平面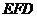 ,
,
∴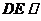 平面
平面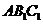 . ……14分
. ……14分
18、解:当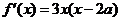 .
……2分
.
……2分
令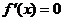 ,得
,得 ,或
,或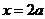 .
.
且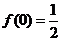 ,
,  .
……6分
.
……6分
(Ⅰ)当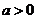 时,
时,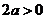 .
.
当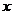 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:
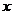 |
 |
0 |
 |
 |
 |
 |
+ |
0 |
- |
0 |
+ |
 |
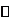 |
 |
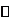 |
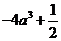 |
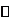 |
……10分
∴ 当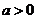 时,在
时,在 处,函数
处,函数 有极大值
有极大值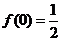 ;在
;在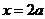 处,函数
处,函数 有极小值
有极小值 .
……12分
.
……12分
(Ⅱ)要使函数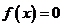 有三个不同的零点,
有三个不同的零点,
必须 .
……14分
.
……14分
解得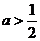 .
.
∴当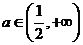 时,函数
时,函数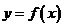 有三个不同的零点.
……16分
有三个不同的零点.
……16分
19、解:(I)每次购买原材料后,当天用掉的400公斤原材料不需要保管费,第二天用掉的400公斤原材料需保管1天,第三天用掉的400公斤原材料需保管2天,第四天用掉的400公斤原材料需保管3天,……第x天(也就是下次购买原材料的前一天)用掉最后的400公斤原材料需保管x-1天.
∴每次购买的原材料在x天内总的保管费用
 (元)……………6分)
(元)……………6分)
(Ⅱ)由上问可知,购买依次原材料的总的费用为 元,
元,
∴购买依次原材料平均每天支付的总费用

∴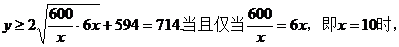 取等号.
取等号.
∴该厂10天购买依次原材料可以使平均每天支付的总费用y最少,为714元.……10分
(Ⅲ)按此优惠条件,则至少15天购买一次原材料,又由上问可知,按此优惠条件购买一次原材料的总的费用为 元,其中x≥15.
元,其中x≥15.
∴购买一次原材料平均每天支付的总费用
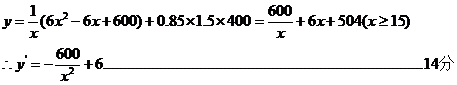
当x≥15时, 上是增函数.
上是增函数.
∴当x=15时,y取最小值,最小值为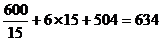 (元)
(元)
∴按此优惠条件,该厂15天购买依次原材料可以使平均每天支付的总费用y最少,最少为634元.……………………………………………………………………16分
20、解:(1)由已知,当n=1时,a13=a12,
又∵a1>0,∴a1=1. …………… 2分
当n≥2时,a13+a23+a33+…+an3=Sn2①
a13+a23+a33+…+an-13=Sn-12② …………… 4分
由①②得,an3=(Sn-Sn-1)(Sn-Sa-1)(Sa+Sa-1)=an(Sn+Sn-1).
∵an>0,∴an2=Sn+Sn-1,
又Sn-1=Sa-aa,∴an2=2Sn-an. 6分
当n=1时,a1=1适合上式.
∴an2=2Sn-an. …………… 7分
(2)由(1)知,an2=2Sn-an,③
当n≥2时,an-12=2Sn-1-an-1,④ …………… 9分
由③④得,an2-an-12=2(Sn-Sn-1)-an+an-1=an+an-1.………… 10分
∵an+an-1>0,∴an-an-1=1,数列{an}是等差数列,首项为1,公差为1. 11分
∴an=n. …………… 12分
(3)∵an=n.,∴bn=3n+(-1)n-1λ.2n.
要使bn+1>bn恒成立,
bn+1-bn=3n+1-3n+(-1)nλ.2n+1-(-1)n-1λ.2n=2×3n-3λ(-1)n-1.2n>0恒成立, 13分
即(-1)n-1λ<( )n-1恒成立.
)n-1恒成立.
ⅰ。当n为奇数时,即λ<( )n-1恒成立.
)n-1恒成立.
又( )n-1的最小值为1.∴λ<1. …………… 14分
)n-1的最小值为1.∴λ<1. …………… 14分
ⅱ。当n为偶数时,即λ>-( )恒成立,
)恒成立,
又-( )n-1的最大值为-
)n-1的最大值为- ,∴λ>-
,∴λ>- . …………… 15分
. …………… 15分
即- <λ<1,又λ≠0,λ为整数,
<λ<1,又λ≠0,λ为整数,
∴λ=-1,使得对任意n∈N*,都有bn+1<bn. …………… 16分