-
网址:http://m.1010jiajiao.com/paper/timu/5155671.html[举报]
10.设P是△ABC内任意一点,S△ABC表示△ABC的面积,λ1=
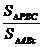 ,
λ2=
,
λ2= ,
,λ3=
 ,定义f(P)=(λ1, λ, λ3),若G是△ABC的重心,f(Q)=(
,定义f(P)=(λ1, λ, λ3),若G是△ABC的重心,f(Q)=( ,
, ,
, ),则 ( )
),则 ( )A. 点Q在△GAB内 B. 点Q在△GBC内
C. 点Q在△GCA内 D. 点Q与点G重合
- 题目来源:高考数学题型训练四 创新题型
参考答案:
一、选择题(每题3分,共30分) 1.D 提示:当x=0时,z=0,当x=1,y=2时,z=6,当x=1,y=3时,z=12,故所有元素之和为18,选D
2.C 提示: A中1-2=-1不是自然数,即自然数集不满足条件;B中1 2=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中
2=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中 不是无理数,即无理数集不满足条件,故选择答案C。
不是无理数,即无理数集不满足条件,故选择答案C。
3.B 提示:根据题意, 是不大于10的正整数、
是不大于10的正整数、 是不大于8的正整数。但是当
是不大于8的正整数。但是当 时
时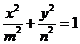 是圆而不是椭圆。先确定
是圆而不是椭圆。先确定 ,
, 有8种可能,对每一个确定的
有8种可能,对每一个确定的 ,
, 有
有 种可能。故满足条件的椭圆有
种可能。故满足条件的椭圆有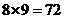 个。选B
个。选B
4.D 提示:由题意至少可得f(0)=f(2)=f(-2)=f(3)=f(-3)=f(-5)=f(5)=f(1)=f(4)=0,即在区间(0,6)内f(x)=0的解的个数的最小值是5,选(D)
5.D 提示:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”;选D。
6.D 提示:(思路一)点P在抛物线y2=2x上,设P( ,y),则有(
,y),则有( +
+ )2=(
)2=( -
-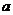 )2+(y-2)2,化简得(
)2+(y-2)2,化简得( -
-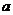 )y2-4y+
)y2-4y+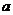 2+
2+ =0, 当
=0, 当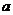 =
= 时, 符合题意;
当a≠
时, 符合题意;
当a≠ 时,∆=0,有
时,∆=0,有 -
- +
+ +
+ =0,(
=0,( 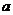 +
+ )(
)(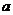 2-
2-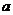 +
+ )=0,
)=0,
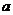 =-
=- 。选D.
(思路二) 由题意有点P在抛物线y2=2x上,B在直线y=2上,当a=-
。选D.
(思路二) 由题意有点P在抛物线y2=2x上,B在直线y=2上,当a=- 时,B为直线y=2与准线的交点,符合题意;当a=
时,B为直线y=2与准线的交点,符合题意;当a= 时,B为直线y=2与抛物线通径的交点,也符合题意,故选D.答案:D
7.C 提示:由 △=p2+4q>0,-q<0,
知方程的根为一正一负.设 f(x)=x2-px-q,则 f(3)=32-3p-q>0, 即 3p+q<9.由于p,q∈N*,所以 p=1,q≤5 或p=2,q≤2.
于是共有7组(p,q)符合题意.故选C.
8.D 提示:设四棱锥的两组不相邻的侧面的交线为 m、n, 直线 m、n 确定了一个平面 β.作与 β 平行的平面 α, 与四棱锥的各个侧面相截,则截得的四边形必为平行四边形.而这样的平面 α 有无数多个.故选D. 答案:D
9。A 提示:∵A=10,B=11,又A×B=10×11=110=16×6+14,∴在16进制中A×B=6E,∴选(A)
时,B为直线y=2与抛物线通径的交点,也符合题意,故选D.答案:D
7.C 提示:由 △=p2+4q>0,-q<0,
知方程的根为一正一负.设 f(x)=x2-px-q,则 f(3)=32-3p-q>0, 即 3p+q<9.由于p,q∈N*,所以 p=1,q≤5 或p=2,q≤2.
于是共有7组(p,q)符合题意.故选C.
8.D 提示:设四棱锥的两组不相邻的侧面的交线为 m、n, 直线 m、n 确定了一个平面 β.作与 β 平行的平面 α, 与四棱锥的各个侧面相截,则截得的四边形必为平行四边形.而这样的平面 α 有无数多个.故选D. 答案:D
9。A 提示:∵A=10,B=11,又A×B=10×11=110=16×6+14,∴在16进制中A×B=6E,∴选(A)
10.A 提示:由题f(p)= 若G为
若G为 .
.
而 与之比较知。
与之比较知。 。故选A。
。故选A。
二、填空题
11.(下列答案中任一即可,答案不唯一)
 (1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的的距离之比为定值。
(1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的的距离之比为定值。
(2)从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的的距离之比为定值。
(3)在空间,从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值。
(4)在空间,射线 上任意一点
上任意一点 到射线
到射线 、
、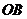 、
、 的距离之比不变。
的距离之比不变。
(5)在空间,射线 上任意一点
上任意一点 到平面
到平面 、
、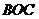 、
、 的距离之比不变。
的距离之比不变。
12.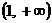 提示:由
提示:由 得
得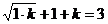 ,解得k=1,所以f(x)=
,解得k=1,所以f(x)= ,f(x)在(0,+∞)内是增函数,故f(x)>1,即f(x)的值域为
,f(x)在(0,+∞)内是增函数,故f(x)>1,即f(x)的值域为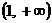
13.259 提示:第1行第1个数为1= ,第2行第1个数为2=
,第2行第1个数为2= ,第3行第1个数为4=
,第3行第1个数为4= ,…,第9行第1个数为
,…,第9行第1个数为 =256,所以第9行第4个数为256+3=259。
=256,所以第9行第4个数为256+3=259。
14.(0.1+p)a 提示:设保险公司要求顾客交x元保险金,若以x表示公司每年的收益额,则x是一个随机变量,其分布列为:
|
x |
x |
x-a |
|
P |
1-p |
p |
因此,公司每年收益的期望值为Ex=x(1-p)+(x-a).p=x-ap.
为使公司收益的期望值等于a的百分之十,
只需Ex=0.1a,即x-ap=0.1a, 故可得x=(0.1+p)a.
即顾客交的保险金为(0.1+p)a时,可使公司期望获益10%a.
15. 提示:由题意得:y=sin3x在
提示:由题意得:y=sin3x在 上的面积为
上的面积为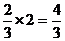 ,
, 在
在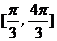 上的图象为一个半周期结合图象分析其面积为
上的图象为一个半周期结合图象分析其面积为 。
。
16.①③④⑤ 提示:如图,B、D、A1到平面 的距离分别为1、2、4,则D、A1的中点到平面
的距离分别为1、2、4,则D、A1的中点到平面 的距离为3,所以D1到平面
的距离为3,所以D1到平面 的距离为6;B、A1的中点到平面
的距离为6;B、A1的中点到平面 的距离为
的距离为 ,所以B1到平面
,所以B1到平面 的距离为5;则D、B的中点到平面
的距离为5;则D、B的中点到平面 的距离为
的距离为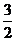 ,所以C到平面
,所以C到平面 的距离为3;C、A1的中点到平面
的距离为3;C、A1的中点到平面 的距离为
的距离为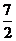 ,所以C1到平面
,所以C1到平面 的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
三、解答题
(17)。(Ⅰ)解:∵ 是函数y=f(x)的图象的对称轴,∴
是函数y=f(x)的图象的对称轴,∴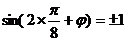 ,∴
,∴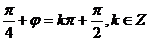 ,∵
,∵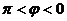 ,∴
,∴ 。
。
(Ⅱ)由(Ⅰ)知 ,因此
,因此 。由题意得
。由题意得 ,所以函数
,所以函数 的单调增区间为
的单调增区间为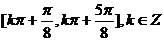 。
。
(Ⅲ)证明:∵|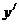 |=|(
|=|( |=|
|=| |≤2
|≤2
所以曲线y=f(x)的切线的斜率取值范围是[-2,2],而直线5x-2y+c=0的斜率为 >2,所以直线5x-2y+c=0与函数
>2,所以直线5x-2y+c=0与函数 的图象不相切。
的图象不相切。
18.解:(I)依题意,得 P0=1,P1= ,
, .
.
(II)依题意,棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第n-2站,又掷出反面,其概率为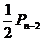 ;第二种,棋子先到第n-1站,又掷出正面,其概率为
;第二种,棋子先到第n-1站,又掷出正面,其概率为
∴
∴
即
(III)由(II)可知数列{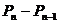 }(1≤n≤99)是首项为
}(1≤n≤99)是首项为 公比为
公比为 的等比数列,
的等比数列,
于是有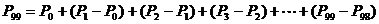
=
因此,玩该游戏获胜的概率为 .
.
19.解:(I)
(II)直线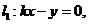 直线
直线 ,由题意得
,由题意得
 即
即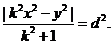
由 知
知
所以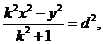 即
即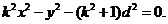
所以动点P的轨迹方程为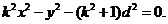
(III)当直线 与
与 轴垂直时,可设直线
轴垂直时,可设直线 的方程为
的方程为 由于直线
由于直线 、曲线C关于
、曲线C关于 轴对称,
轴对称,
且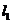 与
与 关于
关于 轴对称,于是
轴对称,于是 的中点坐标都为
的中点坐标都为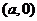 ,所以
,所以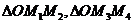
的重心坐标都为 ,即它们的重心重合.
,即它们的重心重合.
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
由 ,得
,得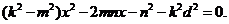
由直线  与曲线C有两个不同交点,可知
与曲线C有两个不同交点,可知 ,且
,且

设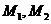 的坐标分别为
的坐标分别为
则
设 的坐标分别为
的坐标分别为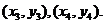
由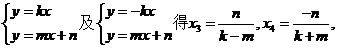
从而
所以
所以
于是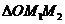 的重心与
的重心与 的重心也重合.
的重心也重合.
20.解答:
(Ⅰ)



 .
.
(Ⅱ)
 ,
,
(Ⅲ)
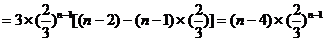
∴  ,
,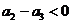 ,
,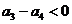 。
。 ,
,
 ,
,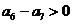 ,等
,等
即在数列 中,
中, 是数列的最大项,所以存在最小的自然数
是数列的最大项,所以存在最小的自然数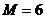 ,对一切
,对一切 都有
都有 <M成立.
<M成立.