-
1.(06年山东)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( )
A.0 B.6 C.12 D.18
-
2.(06年辽宁卷)设+是R上的一个运算, A是R的非空子集,若对任意
 有
有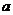 +
+
 ,则称A对运算+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
,则称A对运算+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )A.自然数集 B.整数集 C.有理数集 D.无理数集
-
3.(05天津)从集合{1,2,3,…,11}中的任意取两个元素作为椭圆
 方程中的
方程中的 和
和 ,则能组成落在矩形区域
,则能组成落在矩形区域 内的椭圆的个数是( )
内的椭圆的个数是( )A. 43 B. 72 C. 86 D. 90
-
4.(05福建)
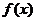 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且 ,则方程
,则方程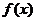 =0在区间(0,6)内解的个数的最小值是 ( )
=0在区间(0,6)内解的个数的最小值是 ( )A. 5 B. 4 C. 3 D. 2
-
5.(06上海卷)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B. 18 C. 24 D.36
-
6.点P到点A(
 ,0),B(
,0),B(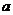 ,2)及到直线x=-
,2)及到直线x=- 的距离都相等,如果这样的点恰好只有一个,那么a的值是 ( )
的距离都相等,如果这样的点恰好只有一个,那么a的值是 ( )
 A.
A. B.
B. C.
C. 或
或 D.-
D.- 或
或 7.如果二次方程 x2-px-q=0(p,q∈N*) 的正根小于3, 那么这样的二次方程有( )
A. 5个 B. 6个 C. 7个 D. 8个
8. 设四棱锥P-ABCD的底面不是平行四边形, 用平面α去截此四棱锥(如右图), 使得截面四边形是平行四边形, 则这样的平面 α ( )
A. 不存在 B. 只有1个
7.如果二次方程 x2-px-q=0(p,q∈N*) 的正根小于3, 那么这样的二次方程有( )
A. 5个 B. 6个 C. 7个 D. 8个
8. 设四棱锥P-ABCD的底面不是平行四边形, 用平面α去截此四棱锥(如右图), 使得截面四边形是平行四边形, 则这样的平面 α ( )
A. 不存在 B. 只有1个 C. 恰有4个 D. 有无数多个 9。(05全国Ⅲ)计算机中常用的十六进制是逢16进1的记数制,采用数字0-9和字母A-F共16个记数符号;这些符号与十进制的数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:E+D=1B,则
 (
)
(
)A .6E B. 72 C .5F D. B0
-
10.设P是△ABC内任意一点,S△ABC表示△ABC的面积,λ1=
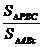 ,
λ2=
,
λ2= ,
,λ3=
 ,定义f(P)=(λ1, λ, λ3),若G是△ABC的重心,f(Q)=(
,定义f(P)=(λ1, λ, λ3),若G是△ABC的重心,f(Q)=( ,
, ,
, ),则 ( )
),则 ( )A. 点Q在△GAB内 B. 点Q在△GBC内
C. 点Q在△GCA内 D. 点Q与点G重合
-
11.在平面几何中有如下特性:从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值。类比上述性质,请叙述在立体几何中相应地特性,并画出图形。不必证明。
类比性质叙述如下 :________________
-
12.规定记号“
 ”表示一种运算,即
”表示一种运算,即 . 若
. 若 ,则函数
,则函数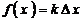 的值域是________.
的值域是________. -
13.一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):
第1行
1
第2行
2 3
第3行
4 5 6 7
…
…
则第9行中的第4个数是________
A.132 B.255 C.259 D.260
-
14.某保险公司新开设了一项保险业务,若在一年内事件E发生,该公司要赔偿a元.设在一年内E发生的概率为p,为使公司收益的期望值等于a的百分之十,公司应要求顾客交保险金为_________________
-
15.(05年湖南)设函数f (x)的图象与直线x =a,x =b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,
 ]上的面积为
]上的面积为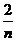 (n∈N*),(i)y=sin3x在[0,
(n∈N*),(i)y=sin3x在[0, ]上的面积为 ;(ii)y=sin(3x-π)+1在[
]上的面积为 ;(ii)y=sin(3x-π)+1在[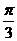 ,
, ]上的面积为 .
]上的面积为 . -
16.
 (06年安徽卷)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面
(06年安徽卷)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面 内,其余顶点在
内,其余顶点在 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面 的距离可能是:①3;
②4; ③5; ④6; ⑤7
的距离可能是:①3;
②4; ③5; ④6; ⑤7以上结论正确的为______________。(写出所有正确结论的编号)
-
(17).(本题满分10分)(05年全国Ⅰ)设函数
 。y=f(x)图像的一条对称轴是直线
。y=f(x)图像的一条对称轴是直线 . (Ⅰ)求
. (Ⅰ)求 ;
;(Ⅱ)求函数
 的单调增区间;
的单调增区间;(Ⅲ)证明直线
 于函数
于函数 的图像不相切.
的图像不相切.18.(本题12分)某人玩硬币走跳棋的游戏,已知硬币出现正、反面的概率都是
 .棋盘上标有第0站、第1站、第2站、……、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
.棋盘上标有第0站、第1站、第2站、……、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为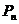 .
.(I)求P0,Pl,P2;(II)求证:

(Ⅲ)求玩该游戏获胜的概率.
-
19.
 (本题12分)(05年北京)如图,直线l1:
(本题12分)(05年北京)如图,直线l1: 与直线l2:
与直线l2: 之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.(Ⅰ)分别用不等式组表示W1和W2;
(Ⅱ)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于M1,M2两点,且与l1,l2分别交于M3,M4两点. 求证△OM1M2的重心与△OM3M4的重心重合.
-
20.(本题12分)设
 轴、
轴、 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是 、
、 ,坐标平面上点
,坐标平面上点 、
、
 分别满足下列两个条件:①
分别满足下列两个条件:①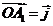 且
且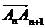 =
= +
+ ;②
;②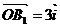 且
且 =
=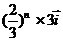 。(Ⅰ)求
。(Ⅰ)求 及
及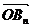 的坐标;
的坐标;(Ⅱ)若四边形
 的面积是
的面积是 ,求
,求
 的表达式;
的表达式;(Ⅲ)对于(Ⅱ)中的
 ,是否存在最小的自然数M,对一切
,是否存在最小的自然数M,对一切 都有
都有 <M成立?若存在,求M;若不存在,说明理由.
<M成立?若存在,求M;若不存在,说明理由.
高考数学题型训练四 创新题型参考答案
参考答案:
一、选择题(每题3分,共30分) 1.D 提示:当x=0时,z=0,当x=1,y=2时,z=6,当x=1,y=3时,z=12,故所有元素之和为18,选D
2.C 提示: A中1-2=-1不是自然数,即自然数集不满足条件;B中1 2=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中
2=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中 不是无理数,即无理数集不满足条件,故选择答案C。
不是无理数,即无理数集不满足条件,故选择答案C。
3.B 提示:根据题意, 是不大于10的正整数、
是不大于10的正整数、 是不大于8的正整数。但是当
是不大于8的正整数。但是当 时
时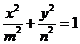 是圆而不是椭圆。先确定
是圆而不是椭圆。先确定 ,
, 有8种可能,对每一个确定的
有8种可能,对每一个确定的 ,
, 有
有 种可能。故满足条件的椭圆有
种可能。故满足条件的椭圆有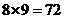 个。选B
个。选B
4.D 提示:由题意至少可得f(0)=f(2)=f(-2)=f(3)=f(-3)=f(-5)=f(5)=f(1)=f(4)=0,即在区间(0,6)内f(x)=0的解的个数的最小值是5,选(D)
5.D 提示:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”;选D。
6.D 提示:(思路一)点P在抛物线y2=2x上,设P( ,y),则有(
,y),则有( +
+ )2=(
)2=( -
-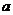 )2+(y-2)2,化简得(
)2+(y-2)2,化简得( -
-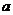 )y2-4y+
)y2-4y+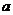 2+
2+ =0, 当
=0, 当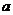 =
= 时, 符合题意;
当a≠
时, 符合题意;
当a≠ 时,∆=0,有
时,∆=0,有 -
- +
+ +
+ =0,(
=0,( 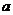 +
+ )(
)(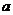 2-
2-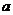 +
+ )=0,
)=0,
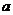 =-
=- 。选D.
(思路二) 由题意有点P在抛物线y2=2x上,B在直线y=2上,当a=-
。选D.
(思路二) 由题意有点P在抛物线y2=2x上,B在直线y=2上,当a=- 时,B为直线y=2与准线的交点,符合题意;当a=
时,B为直线y=2与准线的交点,符合题意;当a= 时,B为直线y=2与抛物线通径的交点,也符合题意,故选D.答案:D
7.C 提示:由 △=p2+4q>0,-q<0,
知方程的根为一正一负.设 f(x)=x2-px-q,则 f(3)=32-3p-q>0, 即 3p+q<9.由于p,q∈N*,所以 p=1,q≤5 或p=2,q≤2.
于是共有7组(p,q)符合题意.故选C.
8.D 提示:设四棱锥的两组不相邻的侧面的交线为 m、n, 直线 m、n 确定了一个平面 β.作与 β 平行的平面 α, 与四棱锥的各个侧面相截,则截得的四边形必为平行四边形.而这样的平面 α 有无数多个.故选D. 答案:D
9。A 提示:∵A=10,B=11,又A×B=10×11=110=16×6+14,∴在16进制中A×B=6E,∴选(A)
时,B为直线y=2与抛物线通径的交点,也符合题意,故选D.答案:D
7.C 提示:由 △=p2+4q>0,-q<0,
知方程的根为一正一负.设 f(x)=x2-px-q,则 f(3)=32-3p-q>0, 即 3p+q<9.由于p,q∈N*,所以 p=1,q≤5 或p=2,q≤2.
于是共有7组(p,q)符合题意.故选C.
8.D 提示:设四棱锥的两组不相邻的侧面的交线为 m、n, 直线 m、n 确定了一个平面 β.作与 β 平行的平面 α, 与四棱锥的各个侧面相截,则截得的四边形必为平行四边形.而这样的平面 α 有无数多个.故选D. 答案:D
9。A 提示:∵A=10,B=11,又A×B=10×11=110=16×6+14,∴在16进制中A×B=6E,∴选(A)
10.A 提示:由题f(p)= 若G为
若G为 .
.
而 与之比较知。
与之比较知。 。故选A。
。故选A。
二、填空题
11.(下列答案中任一即可,答案不唯一)
 (1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的的距离之比为定值。
(1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的的距离之比为定值。
(2)从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的的距离之比为定值。
(3)在空间,从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值。
(4)在空间,射线 上任意一点
上任意一点 到射线
到射线 、
、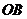 、
、 的距离之比不变。
的距离之比不变。
(5)在空间,射线 上任意一点
上任意一点 到平面
到平面 、
、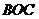 、
、 的距离之比不变。
的距离之比不变。
12.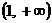 提示:由
提示:由 得
得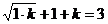 ,解得k=1,所以f(x)=
,解得k=1,所以f(x)= ,f(x)在(0,+∞)内是增函数,故f(x)>1,即f(x)的值域为
,f(x)在(0,+∞)内是增函数,故f(x)>1,即f(x)的值域为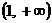
13.259 提示:第1行第1个数为1= ,第2行第1个数为2=
,第2行第1个数为2= ,第3行第1个数为4=
,第3行第1个数为4= ,…,第9行第1个数为
,…,第9行第1个数为 =256,所以第9行第4个数为256+3=259。
=256,所以第9行第4个数为256+3=259。
14.(0.1+p)a 提示:设保险公司要求顾客交x元保险金,若以x表示公司每年的收益额,则x是一个随机变量,其分布列为:
|
x |
x |
x-a |
|
P |
1-p |
p |
因此,公司每年收益的期望值为Ex=x(1-p)+(x-a).p=x-ap.
为使公司收益的期望值等于a的百分之十,
只需Ex=0.1a,即x-ap=0.1a, 故可得x=(0.1+p)a.
即顾客交的保险金为(0.1+p)a时,可使公司期望获益10%a.
15. 提示:由题意得:y=sin3x在
提示:由题意得:y=sin3x在 上的面积为
上的面积为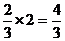 ,
, 在
在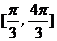 上的图象为一个半周期结合图象分析其面积为
上的图象为一个半周期结合图象分析其面积为 。
。
16.①③④⑤ 提示:如图,B、D、A1到平面 的距离分别为1、2、4,则D、A1的中点到平面
的距离分别为1、2、4,则D、A1的中点到平面 的距离为3,所以D1到平面
的距离为3,所以D1到平面 的距离为6;B、A1的中点到平面
的距离为6;B、A1的中点到平面 的距离为
的距离为 ,所以B1到平面
,所以B1到平面 的距离为5;则D、B的中点到平面
的距离为5;则D、B的中点到平面 的距离为
的距离为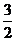 ,所以C到平面
,所以C到平面 的距离为3;C、A1的中点到平面
的距离为3;C、A1的中点到平面 的距离为
的距离为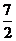 ,所以C1到平面
,所以C1到平面 的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
的距离为7;而P为C、C1、B1、D1中的一点,所以选①③④⑤。
三、解答题
(17)。(Ⅰ)解:∵ 是函数y=f(x)的图象的对称轴,∴
是函数y=f(x)的图象的对称轴,∴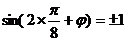 ,∴
,∴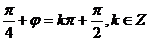 ,∵
,∵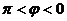 ,∴
,∴ 。
。
(Ⅱ)由(Ⅰ)知 ,因此
,因此 。由题意得
。由题意得 ,所以函数
,所以函数 的单调增区间为
的单调增区间为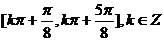 。
。
(Ⅲ)证明:∵|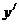 |=|(
|=|( |=|
|=| |≤2
|≤2
所以曲线y=f(x)的切线的斜率取值范围是[-2,2],而直线5x-2y+c=0的斜率为 >2,所以直线5x-2y+c=0与函数
>2,所以直线5x-2y+c=0与函数 的图象不相切。
的图象不相切。
18.解:(I)依题意,得 P0=1,P1= ,
, .
.
(II)依题意,棋子跳到第n站(2≤n≤99)有两种可能:第一种,棋子先到第n-2站,又掷出反面,其概率为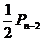 ;第二种,棋子先到第n-1站,又掷出正面,其概率为
;第二种,棋子先到第n-1站,又掷出正面,其概率为
∴
∴
即
(III)由(II)可知数列{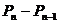 }(1≤n≤99)是首项为
}(1≤n≤99)是首项为 公比为
公比为 的等比数列,
的等比数列,
于是有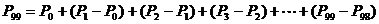
=
因此,玩该游戏获胜的概率为 .
.
19.解:(I)
(II)直线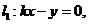 直线
直线 ,由题意得
,由题意得
 即
即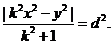
由 知
知
所以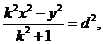 即
即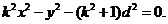
所以动点P的轨迹方程为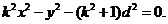
(III)当直线 与
与 轴垂直时,可设直线
轴垂直时,可设直线 的方程为
的方程为 由于直线
由于直线 、曲线C关于
、曲线C关于 轴对称,
轴对称,
且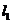 与
与 关于
关于 轴对称,于是
轴对称,于是 的中点坐标都为
的中点坐标都为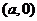 ,所以
,所以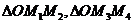
的重心坐标都为 ,即它们的重心重合.
,即它们的重心重合.
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
由 ,得
,得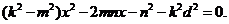
由直线  与曲线C有两个不同交点,可知
与曲线C有两个不同交点,可知 ,且
,且

设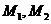 的坐标分别为
的坐标分别为
则
设 的坐标分别为
的坐标分别为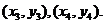
由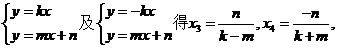
从而
所以
所以
于是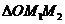 的重心与
的重心与 的重心也重合.
的重心也重合.
20.解答:
(Ⅰ)



 .
.
(Ⅱ)
 ,
,
(Ⅲ)
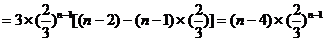
∴  ,
,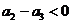 ,
,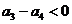 。
。 ,
,
 ,
,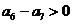 ,等
,等
即在数列 中,
中, 是数列的最大项,所以存在最小的自然数
是数列的最大项,所以存在最小的自然数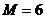 ,对一切
,对一切 都有
都有 <M成立.
<M成立.