-
网址:http://m.1010jiajiao.com/paper/timu/5155369.html[举报]
22.(本小题满分12分)
 如图:已知椭圆
如图:已知椭圆 是长轴的一个端点,弦BC过椭圆的中心O,且
是长轴的一个端点,弦BC过椭圆的中心O,且 .
.(1)求椭圆的方程;
(2)若AB上的一点F满足

求证:CF平分∠BCA;
(3)对于椭圆上的两点P、Q,∠PCQ的平分线总是垂直于x轴时,是否存在实数λ,使得

- 题目来源:高考预测理科数学试卷 参考公式: 如果事件A、B互斥,那么 球的表面积公式 P(A+B)=P(A)+P(B) S=4πR2 如果事件A、B相互独立, 其中R表示球的半径 那么P(A.B)=P(A).P(B) 球的体积公式 如果事件A在一次试验中发生的概率 是P,那么n次独立重复试验中恰好发 其中R表示球的半径 生k 次的概率P
参考答案
一、选择题:
1-5BCAAB 6-10BABBD 11-12AC
二、填空题:
11.8
12.-2 13.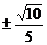 14.-9 15.
14.-9 15. 16.1
16.1
三、解答题:
17.解:(1)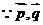 共线
共线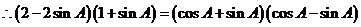 …….2’
…….2’
 ……………2’ 而
……………2’ 而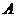 为锐角,所以
为锐角,所以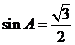
 …...2’
…...2’
(2)
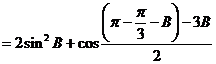
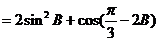
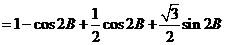

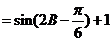 …………..3’
…………..3’

 时,
时,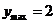 ………….4’
………….4’
18.解:(1)事件 只能是“四次取球中出现三次白球一次黑球”,
只能是“四次取球中出现三次白球一次黑球”,
每次取得白球的概率为 ;取得黑球的概率是
;取得黑球的概率是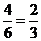 …………..2’
…………..2’
于是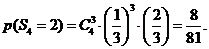 ………………………………..2’
………………………………..2’
(2) 可能的取值有
可能的取值有
 ;
;
 ;
;
 ;
;
 ;
;
 ,…………………5’
,…………………5’
 |
 |
 |
0 |
2 |
4 |
 |
 |
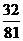 |
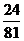 |
 |
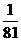 |
于是 取值的分布列为
取值的分布列为
………………………………………….2’
 …………2’
…………2’
19.(1)
(2)∠CEA为二面角A-PD-C的平面角,
(3)点B到平面PDC的距离为
20.解:(1)
 是首项a1,公差d=3的等差数列
是首项a1,公差d=3的等差数列

(2)
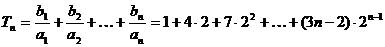
2Tn=1.2+4.22+7.22+…+(3n-2).2n
两式相减-Tn=1+3(2+22+…+2n-1)-(3n-2).2n
=-5-(3n-5).2n
∴Tn=(3n-5).2n+5
21.解:(1)
所求切线斜率为 
切线 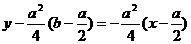
令y=0 得x=b ∴函数y=f(x)过点P的切线过点(b,0)
(2)
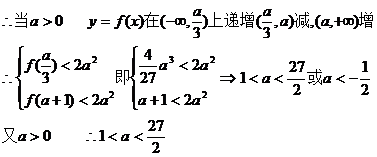
当a<0时,函数y=f(x)在( ,+∞)上递增
,+∞)上递增
∴f(1-a)<2a2.即(1-a)(1-a-a)2<2a2 4a3-6a2+5a-1>0
4a3-6a2+5a-1>0
令g(a)=4a3-ba2+5a-1
g′(a)=12a2-12a+5=12(a- )2+2>0
)2+2>0
∴g(a)在(-∞,0)单增 又g(0)=-1<0 ∴g(a)>0无解
综上 1<a<
22.(I)解: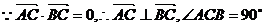
又
∴△AOC是等腰直角三角形
∵A(2,0),∴C(1,1)而点C在椭圆上,
∴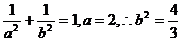
∴所求椭圆方程为
(Ⅱ)证明C(1,1),则B(-1,-1)
又
即点F分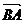 所成的定比为2.
所成的定比为2.
设
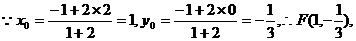
CF⊥x轴,
∴∠ACF=∠FCB=45°,即CF平分∠BCA.
(Ⅲ)对于椭圆上两点P、Q,∵∠PCQ的平分线总是垂直于x轴
∴PC与CQ所在直线关于x=1对称,kpC=k,则kcQ=-k,
设C(1,1),则PC的直线方程y-1=k(x-1) y=k(x-1)+1
①
y=k(x-1)+1
①
QC的直线方y-1=-k(x-1)  y=-k(x-1)+1 ②
y=-k(x-1)+1 ②
将①代入 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 ③
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 ③
∵C(1,1)在椭圆上,∴x=1是方程③的一个根,
∴xp.1= =1同理将②代入x2+3y2=4得
=1同理将②代入x2+3y2=4得
(1+3k2)x2-6k(k+1)x+3k2+6k-1=0 ④
∵C(1,1)在椭圆上,
∴x=1是方程④的一个根,
∴xQ.1= 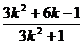
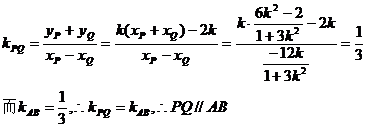
∴存在实数λ,使得 .
.