-
1.已知集合
 ,函数
,函数 的定义域为B,则
的定义域为B,则 ________
________ -
2.不等式
 的解集为___________.
的解集为___________. -
3. 函数y=1og2(x2+2)(x≤0)的反函数是_________________.
-
4.已知复数
 且
且 是实数,则实数
是实数,则实数
-
5.函数
 的最小正周期是____________.
的最小正周期是____________. -
6.以抛物线
 的焦点
的焦点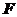 为右焦点,且两条渐近线是
为右焦点,且两条渐近线是 的双曲线方程为___________________.
的双曲线方程为___________________. -
7.在极坐标系中,点
 到圆
到圆 上动点的距离的最大值为________.
上动点的距离的最大值为________. -
8. 函数
 则方程
则方程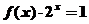 的实根的个数是_________.
的实根的个数是_________.
-
9.特奥会期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为___________.
-
10.设
 是
是
其中
 分别是
分别是
的最小值是_______________.
-
11.已知
 是定义在
是定义在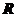 上的不恒为零的函数,且对于任意的
上的不恒为零的函数,且对于任意的 ,满足
,满足 ,
, 考查下列结论:(1)
考查下列结论:(1) ;(2)
;(2) 为偶函数;(3)数列
为偶函数;(3)数列 为等比数列;(4)
为等比数列;(4) 。其中正确的是__________。
。其中正确的是__________。 -
12.
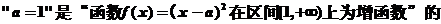 ( )
( )A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要。
-
13.已知函数
 的图象按向量
的图象按向量 平移得到函数
平移得到函数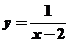 的图象,则函数
的图象,则函数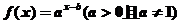 的反函数
的反函数 的图象恒过定点 ( )
的图象恒过定点 ( )A.(2,1) B.(1,2) C.(-2,1) D.(0,2)
-
14.已知直线m、n及平面
 ,其中m∥n,那么在平面
,其中m∥n,那么在平面 内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集。其中正确的是( )
内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集。其中正确的是( )A、(1)(2)(3) B、(1)(4) C、(1)(2)(4) D、(2)(4)
-
15.一机器猫每秒钟前进或后退一步,程序设计师让机器猫以前进3步,然后再后退2步的规律移动。如果将此机器猫放在数轴的原点,面向正方向,以1步的距离为1单位长移动。令P(n)表示第n秒时机器猫所在位置的坐标,且P(0)=0,则下列结论中错误的是 ( )
A.P(3)=3 B.P(5)=1 C.P(101)=21 D.P(101)> P(104)
-
16.(本题满分12分)已知
 是
是 中
中 的对边,若
的对边,若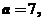
 求边长
求边长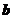 及
及 外接圆半径
外接圆半径

-
17.(本题满分14分)
直三棱柱ABC-A1B1C1的底面为等腰直角三角形,
 BAC=900,AB=AC=2,AA
BAC=900,AB=AC=2,AA =2
=2 ,E, F分别是BC、AA1的中点。求(1)异面直线EF和A1B所成的角。
,E, F分别是BC、AA1的中点。求(1)异面直线EF和A1B所成的角。 (2)直三棱柱ABC-A1B1C1的体积。
(2)直三棱柱ABC-A1B1C1的体积。 -
18. (本题满分14分)某地区由于战争的影响,据估计,将产生60~100万难民,联合国难民署从4月1日起为该地区难民运送食品. 连续运送15天,总共运送21300 t;第一天运送1000 t,第二天运送1100 t,以后每天都比前一天多运送100 t,直到达到运送食品的最大量,然后再每天递减100 t;求在第几天达到运送食品的最大量.
-
19. (本题满分14分)已知函数
 (常数
(常数 )
)(1)求函数
 的定义域,判断
的定义域,判断 的奇偶性并说明理由.
的奇偶性并说明理由.(2)试研究函数
 在定义域内的单调性,并利用单调性的定义给出证明。
在定义域内的单调性,并利用单调性的定义给出证明。 -
20. (本题满分18分)已知F1、F2分别是椭圆
 的左、右焦点,P是此椭圆上的一动点,并且
的左、右焦点,P是此椭圆上的一动点,并且 的取值范围是
的取值范围是
(1) 求此椭圆的方程;
(2) 点A是椭圆的右顶点,直线y = x与椭圆交于B、C两点(C在第一象限内),又P、Q是椭圆上两点,并且满足
 ,求证:向量
,求证:向量 共线.
共线. -
21.(本题满分18分)
已知向量
 ,其中
,其中 ,
,
 ,
,把其中
 所满足的关系式记为
所满足的关系式记为 ,若函数
,若函数 为奇函数.
为奇函数. (Ⅰ) 求函数
 的表达式;
的表达式;(Ⅱ) 已知数列
 的各项都是正数,
的各项都是正数,  为数列
为数列 的前
的前 项和,且对于任意
项和,且对于任意 ,都有“
,都有“ 的前
的前 项和等于
项和等于 ,”求数列
,”求数列 的通项式;
的通项式;(Ⅲ) 若数列
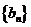 满足
满足 ,求数列
,求数列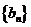 的最小值.
的最小值.