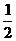-
1.
 的虚部是( )
的虚部是( )A、-i B、i C、-1 D、1
2已知全集U=Z,A={-2,-1,0,1},B={x |
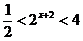 ,x∈Z},则
,x∈Z},则 ( )
( )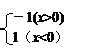 A、{0,1} B、{1} C、{-2,-1} D、{-1,0,1}
A、{0,1} B、{1} C、{-2,-1} D、{-1,0,1} -
3.设函数f(x)= ,则
 的值为
的值为A、a B、b C、min{a,b}.D、max{a,b}
-
4.设命题p:f(x)=lnx+x2+ax+1在(0,+∞)内单调递增,命题q:a≥-2,则p是q的( )
A、充分不必要条件 B、必要不充分条件
C、充分必要条件 D、既不充分又不必要条件
-
5.若
 展开式的第五项是常数项,则此展开式所有项的系数之和为( )
展开式的第五项是常数项,则此展开式所有项的系数之和为( )A、-64 B、64 C、
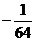 D、
D、
-
6.
 ( )
( )A、-6 B、6 C、-12 D、12
-
7.已知定义在R上的函数y=f(x)存在反函数y= f-1(x),若函数y=f(x+1)的反函数是f-1(x-1),且f(0)=1,则f(12)=
A、1 B、一1 C、13 D、14
-
8.有下列命题:
①若sin θ+cosθ=
 ,则
,则
②关于实数x的方程sinx=x有三个解:
③若角,β满足cosα cosβ=1,则sin(α+β)=0;
④函数f(x)=sinx+sin|x |的值域为[-2,2];
其中真命题有( )个
A、1 B、2 C、3 D、4
-
9.12支足球队(含甲、乙、丙)平均分成三个小组,甲、乙、丙三个球队中至少有两支球队被分在同一小组的概率是( )
A、
 B、
B、 C、
C、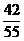 D、
D、
-
10.在三棱锥P-ABC中,∠APB=∠BPC=60°,PA=1,PB =
 ,PC=
,PC= ,则三棱锥P-ABC的体积为( )
,则三棱锥P-ABC的体积为( )A、
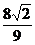 B、
B、 C、
C、 D、
D、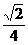
-
11.椭圆C1:
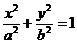 的左准线为l,左、右焦点为分别为F1、F2,抛物线C2的准线为l,焦点为F2,C1与C2的一个交点为P,线段PF2的中点为G,O是坐标原点,则
的左准线为l,左、右焦点为分别为F1、F2,抛物线C2的准线为l,焦点为F2,C1与C2的一个交点为P,线段PF2的中点为G,O是坐标原点,则 的值为( )
的值为( )A、-1 B、1 C、-
 D、
D、
-
12.底面边长为1、侧棱长为2的正四棱柱ABCD-AlBlClDl的8个顶点都在球O的表面上,E是侧棱AAl的中点,F是正方形ABCD的中心,则直线EF被球O截得线段长为( )
A、
 B、
B、 c、
c、 D、
D、
第Ⅱ卷(非选择题,共90分)
-
13.某市有300名学生参加数学竞赛的预赛,竞赛成绩宇服从正态分布ξ~N(80,100),若规定,预赛成绩在95分或95分以上的学生参加复赛,估计进入复赛的人数是 (参考数据:Φ(0.15)=0.5596,Φ(1.5)=0.9332,Φ(0.8)=0.7881)
-
14.函数y=tan2x在x=
 处的切线方程为
(结果写成直线方程的一般式)
处的切线方程为
(结果写成直线方程的一般式) -
15.已知在平面直角坐标系中O(0,0)、M(1,0)、N(1,1)、Q(2,3)动点P(x,y)满足不等式1≤
 ≤3,2 ≤
≤3,2 ≤ ≤4,则ω=
≤4,则ω= 的最大值为
的最大值为
-
16.以下四个关于圆锥曲线的命题中:
①平面内到定点A(1,0)和定直线l:x=2的距离之比为
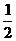 的点的轨迹方程是:
的点的轨迹方程是:
②点P是抛物线y2=2x上的动点,点P在y轴上的射影是M,点A的坐标是A(3,6),则
|PA|+|PM|的最小值是6;
③平面内到两定点距离之比等于常数λ(λ>0)的点的轨迹是圆;
④若过点C(1,1)的直线l交椭圆
 于不同的两点A、B,且C是AB的中点,则直线l的方程是3x+4y-7=0:
于不同的两点A、B,且C是AB的中点,则直线l的方程是3x+4y-7=0:其中真命题的序号是 (写出所有真命题的序号)
-
17.
 (本小题满分12分)已知函数f(x)=(4cos2x-2)(cos 2x+2sinxcosx)
(本小题满分12分)已知函数f(x)=(4cos2x-2)(cos 2x+2sinxcosx)(1)求 f(x)的最小正周期;
(2)在给出的直角坐标系中画出y= f(x) 在区间[-
 ,
,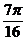 ]上的简图.(要求先列表,再描点画图)
]上的简图.(要求先列表,再描点画图) -
18.(本小题满分12分)已知函数f(x) =ax3+bx2+cx+d(x∈R)在x=
 时取极小值-6
时取极小值-6 ,且函数y=f(x+
,且函数y=f(x+ )的图象关于点(-
)的图象关于点(- ,0)对称.
,0)对称.
(1)求函数f(x)的解析式:
(2)设g(x)=10x+m,x∈[-1,1],若对于任意α1∈[-1,1]总存在α 2∈[-1,1],使g(α 2)=f(α1),求实数m的取值范围;
-
19.(本小题满分12分)如图,已知梯形ABB1E中EB1∥AB和正方形BB1 C1C且AC=BlCl=2,
 CCl⊥平面EBlCl,D是BBl的中点,F是AB的中点,∠ACB=∠AED=90°
CCl⊥平面EBlCl,D是BBl的中点,F是AB的中点,∠ACB=∠AED=90°(1)求证CF⊥平面ABBlE;
(2)求异面直线AC与ECl所成的角的大小;
(3)求二面角E-AC1-C的大小:
-
20.(本小题满分12分)设b,c分别是先后抛掷一枚骰子得到的点数,A={x|x2-bx+3c≤0,x∈N*}.
(1)求A中恰有5个元素的概率;
(2)用随机变量ξ表示A中元素的个数,求ξ的分布列及期望:
-
21.(本小题满分12分)已知直线l:x一
 +4=0与椭圆C:
+4=0与椭圆C: (a>0,b>0)有且仅有一个公共点G,直线l与x轴交于E点,直线l与y轴交于F点,且
(a>0,b>0)有且仅有一个公共点G,直线l与x轴交于E点,直线l与y轴交于F点,且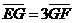
(1)求椭圆C的方程:
(2)若直线m绕点E旋转,且保持与(1)中所求的椭圆C相交于不同两点A、B,求线段AB中点P的轨迹方程.
-
22.(本小题满分14分)已知数列{an} 满足a1 =
 , an+1 =
, an+1 = (n=1,2,…)
(n=1,2,…) (1)求数列{an}的通项
(2)设数列{bn}满足an (bn + a1)=1,
求证:对任意,n>1,n∈N*,bn+1 + bn+2+…+ b2n+ b4n+1<