-
1. 直线l经过A(2,1)、B(1,m2)(m∈R)两点,那么直线l的倾斜角的取值范围是( )
A.
 B.
B.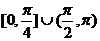 C.
C. D.
D.
-
2. 已知点A(6,-4),B(1,2)、C(x,y),O为坐标原点,若
 则点C的轨迹方程是
(
)
则点C的轨迹方程是
(
)A.2x-y+16=0 B.2x-y-16=0 C.x-y+10=0 D.x-y-10=0
-
3. 若点(5,b)在两条平行直线6x-8y+1=0与3x-4y+5=0之间,则整数b的值为( )
A.5 B.-5 C.4 D.-4
-
4.直线ax+by+b-a=0与圆x2+y2-x-2=0的位置关系是 ( )
A.相离 B.相交 C.相切 D.与a,b的取值有关
-
5.已知直线ax+3y+1=0与直线x+(a-2)y+a=0,当a=_________时,两直线平行;当a=_________时,两直线重合;当a∈_____________________________时,两直线相交.
-
6.将直线y=-
 x+2
x+2 绕点(2,0)按顺时针方向旋转30°所得直线方程是______
绕点(2,0)按顺时针方向旋转30°所得直线方程是______ -
7.在坐标平面内,由不等式组
 所确定的平面区域的面积为________
所确定的平面区域的面积为________ -
8.已知定点P(2,1),分别在y=x及x轴上各取一点B与C,使
 BPC的周长最小,最小值为_________
BPC的周长最小,最小值为_________ -
9.经过点M(1,3)的圆x2+y2=1的切线方程是________________
-
10.若圆经过点A(a,0),B(2a,0),C(0,a)(a≠0),则这个圆的方程为_______________
-
11.一直线被两条平行直线x+2y-1=0及x+2y-3=0所截的线段的中点在直线x-y-1=0上,且这条直线与两平行线的夹角为45°,求此直线的方程.
-
12.当C为何值时,圆x2+y2+x-6y+C=0与直线x+2y-3=0的两交点P、Q满足OP⊥OQ?(其中O为坐标原点)
-
13.已知圆C:x2+(y-2)2=5,直线l:mx-y+1=0,
(1)求证:对m∈R,直线l与圆C总有两个不同交点;
(2)设l与圆C交于A、B两点,若|AB|=
 ,求l的倾斜角;
,求l的倾斜角;(3)求弦AB的中点M的轨迹方程.
-
14.圆的方程为x2+y2-6x-8y=0,过坐标原点作长为8的弦,求弦所在的直线方程。
-
15.已知定点A(0,1),B(0,-1),C(1,0)。动点P满足:
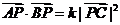 。
。⑴求动点P的轨迹方程,并说明方程表示的曲线;
⑵当
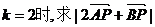 的最大值和最小值。
的最大值和最小值。 -
16.已知圆M:2x2+2y2-8x-8y-1=0和直线l:x+y-9=0过直线 上一点A作△ABC,使∠BAC=45°,AB过圆心M,且B,C在圆M上。
⑴当A的横坐标为4时,求直线AC的方程;
⑵求点A的横坐标的取值范围。
答案:1-4 BBCB 5. 3, -1,
 6.x=2
6.x=2 -
7. 16 8.
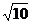 9.
4x-3y+5=0或x=1
9.
4x-3y+5=0或x=1 -
10.
 11. 3x-9y-1=0或9x+3y-13=0
11. 3x-9y-1=0或9x+3y-13=0 -
12. c=3 13. (2)30o或150o (3)
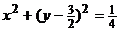
-
14.x=0或

-
15.(1)k=1时 x=1 k≠1时
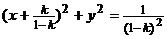 (2)
(2)
-
16.(1)5x+y-25=0或x-5y+21=0 (2) [3,6]