-
1、已知集合
 集合
集合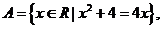 则
则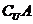 等于( )
等于( ) A、
 B、
B、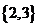 C、
C、 D、
D、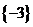
-
2、“
 ”是“
”是“ ”的
”的A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
-
3、若平面四边形ABCD满足
 ,
, ,则该四边形一定是
,则该四边形一定是A、直角梯形 B、矩形 C、菱形 D、正方形
-
4、函数
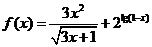 的定义域是( )
的定义域是( )A、
 B、
B、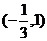 C、
C、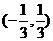 D、
D、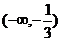
-
5、已知数列{an},首项
 ,它的前n项和为Sn,若
,它的前n项和为Sn,若
 ,且A、B、
,且A、B、C三点共线(该直线不过原点O),则S20=( )
A、170 B、 101 C、200 D、210
-
6、
 在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A、1∶
 B、1∶9
B、1∶9 C、1∶
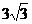 D、1∶
D、1∶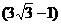
-
7、由函数
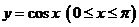 图象与直线
图象与直线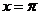 及
及 的
的图象围成一个封闭图形的面积是 ( )
A、1 B、
 C、2
D、
C、2
D、
-
8、在直角坐标系中,函数

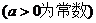 所表示的曲线叫箕舌线,则箕舌线可
所表示的曲线叫箕舌线,则箕舌线可能是下列图形中的
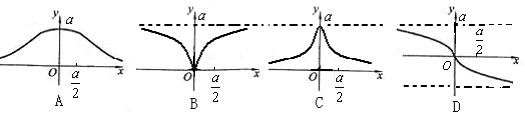
-
9、已知l,m,表示直线,
 表示平面,下列条件中能推出结论的正确的是:
表示平面,下列条件中能推出结论的正确的是:条件:①l⊥m, l⊥
 , m⊥
, m⊥ ; ②
; ②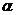 ∥
∥ ,
,  ∥
∥ ; ③l⊥
; ③l⊥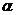 ,
, 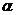 ∥
∥ ;④ l⊥
;④ l⊥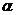 , m⊥
, m⊥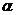
结论:a: l ⊥
 b:
b: 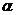 ⊥
⊥ c: l∥m
d:
c: l∥m
d: 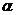 ∥
∥
A、①
 a,②
a,② b,③
b,③ c,④
c,④ d
B、①
d
B、① b,②
b,② d,③
d,③ a,④
a,④ c
cC、①
 c,②
c,② d,③
d,③ a,④
a,④ b
D、①
b
D、① d,②
d,② b,③
b,③ a,④
a,④ c
c -
10、已知数列
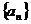 为等比数列,
为等比数列, ,又第
,又第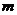 项至第
项至第 项的和为112
项的和为112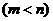 ,
,则
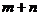 的值为
的值为A. 11 B. 12 C. 13 D. 14
-
11、以正方体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形,从中随机取出两个三
角形,则这两个三角形共面的概率为
A、 B、 C、 D、
-
12、已知椭圆+=1上有n个不同的点P1,P2,P3,…,Pn.设椭圆的右焦点为F,数列{|PnF|}是公差不小于
 的等差数列,则n的最大值为
的等差数列,则n的最大值为 A、2006 B、2007 C、2008 D、1004
第Ⅱ卷(非选择题 共90分)
-
13、一个田径队,有男运动员56人,女运动员42人,比赛后,立即用分层抽样的方法,从
全体队员中抽出一个容量为28的样本进行尿样兴奋剂检查,其中男运动员应抽 人.
-
14、函数f(x)=ax3+bx2+cx+d的部分数值如下:
x
-3
-2
-1
0
1
2
3
4
5
6
y
-80
-24
0
4
0
0
16
60
144
296
则函数y=lgf(x)的定义域为___________.
-
15、设{an}为等差数列,从{a1,a2,a3,…,a10}中任取4个不同的数,使这4个数仍成等
差数列,则这样的等差数列最多有 个.
-
16、定义点
 到直线
到直线 的有向距离为:
的有向距离为: .已知点
.已知点 、
、 到直线
到直线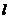 的有向距离分别是
的有向距离分别是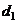 、
、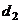 ,有以下命题:
,有以下命题:①若

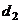 =0,则直线
=0,则直线
 与直线
与直线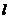 平行;②若
平行;②若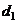 +
+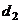 =0,则直线
=0,则直线
 与直线
与直线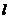 平行;
平行;③若
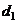 +
+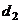 =0,则直线
=0,则直线
 与直线
与直线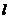 垂直;④若
垂直;④若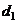
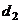 <0,则直线
<0,则直线
 与直线
与直线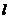 相交。
相交。以上结论正确的是 .(要求填上正确结论的序号)
-
17、(本题满分12分)
已知函数
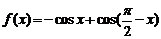 ,
,⑴ 若
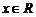 ,求函数
,求函数 的最大值与最小值。
的最大值与最小值。⑵ 若
 ,且
,且 ,求
,求 的值。
的值。 -
18、(本题满分12分)
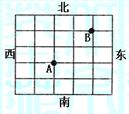 如图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、南、北四个方向之一行走。若甲向东、向西行走的概率均为
如图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、南、北四个方向之一行走。若甲向东、向西行走的概率均为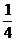 ,向南、向北行走的概率分别为
,向南、向北行走的概率分别为 和p,乙向东、南、西、北四个方向行走的概率均为q
和p,乙向东、南、西、北四个方向行走的概率均为q⑴ 求p和q的值;
⑵ 设至少经过t分钟,甲、乙两人能首次相遇,试确定t的值,并求t分钟时,甲乙两人相遇的概率.
-
19、(本题满分12分)
设函数
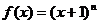 (n∈N),且当x=
(n∈N),且当x= 时,f(x)的值为17+12
时,f(x)的值为17+12 ;
; (a≠1,a∈R),定义:
(a≠1,a∈R),定义: =
=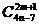
 -
-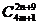
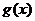 .
.(1)当a =-1时,
 的表达式.
的表达式.(2)当x ∈[0,1]时,
 的最大值为-65,求a的值.
的最大值为-65,求a的值. -
20、(本题满分12分)
如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,
⑴ 求点E、F在该球面上的球面距离;
 ⑵ 求平面OEF与平面OBC所成的锐二面角。(用反三角函数表示)
⑵ 求平面OEF与平面OBC所成的锐二面角。(用反三角函数表示) -
21、(本题满分12分)
在m(m≥2)个不同数的排列
 …
… 中,若1≤i<j≤m时, Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列
中,若1≤i<j≤m时, Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列 的逆序数为an,例如排列21的逆序数
的逆序数为an,例如排列21的逆序数 ,排列321的逆序数
,排列321的逆序数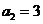 ,排列4321的逆序数
,排列4321的逆序数 。
。(1)求a4、a5,并写出an的表达式;
(2)令
 ,证明:
,证明: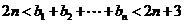 ,n=1,2,….
,n=1,2,…. -
22.(本题满分14分)
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且
满足
 .
.⑴ 当点P在y轴上移动时,求点M的轨迹G;
⑵ 过点T(-1,0)作直线l与轨迹G交于A、B两点,若在x轴上存在一点E(x0,0),
使得
 ABE是等边三角形,求x0的值.
ABE是等边三角形,求x0的值.
高考文科数学仿真测试卷 文科数学(一) 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。 参考公式: 如果事件A、B互诉,那么: 如果事件A、B相互独立,那么 如果事件A在一次试验中发生的概率是P,那行n次独立重复试验中恰好发生k次的概率是: 球的表面积公式:其中R表示球的半径. 球的体积公式:,其中R表示球的半径. 区域作答。 3.考试结束,监考人员将第Ⅰ卷和第Ⅱ卷一并收回。 第Ⅰ卷(选择题 共60分)参考答案
参考答案:
一、选择题(本大题共2小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
B |
C |
B |
A |
D |
B |
A |
B |
B |
D |
B |
简答与提示
1、
2、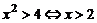 或
或 ,
,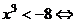
 ;
;
3、
 是平行四边形,
是平行四边形, ;
;
4、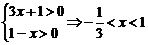 ;
;
5、A、B、C三点共线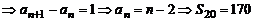 ;
;
6、面积比是相似比的平方,体积比是相似比的立方;
7、根据对称性;
8、①函数是偶函数,②函数先单调递增后单调递减,③当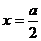 时,
时, ;
;
9、根据线线、线面、面面平行和垂直的有关判定逐个判断即可;
10、依题意: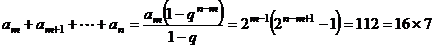 ;
;
11、以正方体ABCD-A′B′C′D′的任意三个顶点为顶点可作 (个)三角形,正方体
(个)三角形,正方体
的表面及对角面每个面有 =4(个)三角形,所以所求概率为
=4(个)三角形,所以所求概率为 ;
;
12、椭圆+=1中, ,所以(|PnF|)min=
,所以(|PnF|)min= (|PnF|)max=
(|PnF|)max=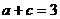
所以 .
.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在横线上。)
13、16 14、(-1,1)和(2,+∞)
15、24 16、④
简答与提示:
13、一个田径队,有男运动员56人,女运动员42人,比赛后,立即用分层抽样的方法,从
全体队员中抽出一个容量为28的样本进行尿样兴奋剂检查,其中男运动员应抽 人.
14、解:由f(x)的解析式可知f(x)图象连续及f(x)的单调性可确定,
在(-1,1)和(2,+∞)上均有f(x)>0.
15、设{an}公差为d,则后取四个数的公差 或
或 或
或 ,它们分别有14、
,它们分别有14、
8、2种取法,所以共有24个
16、当
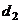 =0,①不对;若
=0,①不对;若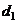 +
+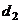 =0,点
=0,点 、
、 在直线
在直线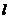 上或在直线
上或在直线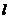 的异侧,所以
的异侧,所以
②③错;
三、解答题
17、(本题满分12分)
解:① 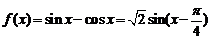 ,
,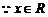 ,
, ,
,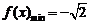
②
解一、 ,
,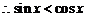 ,
,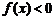 ,又
,又 ,
,
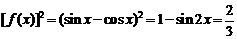 ,
,  。
。
解二、 ,
, ,
,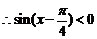 ,
, ,
,
 ,
, ,
, 。
。
18、(1) …………………4分
…………………4分
(2)t=2甲、乙两人可以相遇(如图,在C、D、E三处相遇) …………………5分
|
PC= …………………7分
…………………7分
PD= …………………9分
…………………9分
PE=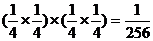 ……………………11分
……………………11分
PC+PD+PE= 即所求的概率为
即所求的概率为 。 ……12分
。 ……12分
19、(本小题满分12分)
解:∵f(x)=(x +1)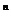 ,
f(
,
f( )= 17+12
)= 17+12 , ∴n= 4 ………………………2分
, ∴n= 4 ………………………2分
又∵ , ∴m= 4, ∴F(x)=(x+1)
, ∴m= 4, ∴F(x)=(x+1)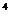 -(x+a)
-(x+a)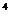 …………4分
…………4分
(1)当a =-1时,F(x)=(x +1)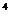 -(x +a)
-(x +a)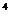 =8x
=8x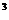 +8x ………………………6分
+8x ………………………6分
(2)∵
∵F (x)=12(1-a)x
(x)=12(1-a)x +12(1-a
+12(1-a )x +4(1-a
)x +4(1-a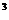 ) ………………………8分
) ………………………8分
△=[12(1-a )]
)] -4.12(1-a).4(1-a
-4.12(1-a).4(1-a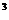 )
)
=-48(1-a)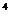 <
0
(a≠1)
<
0
(a≠1)
Ⅰ)当1-a >0时,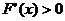 ,F(x)为增函数.∵x∈[0,1]
,F(x)为增函数.∵x∈[0,1]
∴F(1)=-65 ∴2 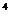 -(1+a)
-(1+a)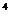 =-65
=-65
∴1+a=±3 ∴a =-4 a=2(舍去)
Ⅱ) 当1-a <0时, ,F(x)为减函数.
,F(x)为减函数.
∴F(0)=-65 ∴1 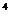 -a
-a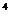 =-65 ∴a =
=-65 ∴a =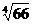 a =-
a =-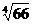 (舍去)
(舍去)
综上:a =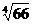 或a =-4 ……………………………………………………………12分
或a =-4 ……………………………………………………………12分
20、(本题满分12分)
解:⑴解法一:如图1,证明0M=0N=MN= AB=
AB= BC=
BC= AC,从而∠MON=
AC,从而∠MON=
∴点E、F在该球面上的球面距离为 .
.
解法二:如图2,补形易证:∠EOF=∠GOH = .
.
解法三:其实 ,易证:∠EOF=
,易证:∠EOF= .
.
解法四:如图3,建立空间直角坐标系,易知E( ,0,
,0,  )、F(0,
)、F(0, ,
,  )
)
∴ ,从而∠EOF =
,从而∠EOF = . …………………6分
. …………………6分
 |
⑵ 解法一:如图1,取BC中点P,连接AP交MN与Q,则易证,∠POQ就是所求二面角的平面角。
在三角形OPQ中,OP= ,PQ=OQ=
,PQ=OQ= AP=
AP= ,可解得cos∠POQ=
,可解得cos∠POQ= ,
,
∴∠POQ=arcos (=arctan
(=arctan ).
……………………………12分
).
……………………………12分
解法二:如图2,补形成正方体去解决.
解法三:如图3,建立空间直角坐标系去求解。
21.(本小题共12分)
解:
(1)由已知得 ,
, .
.
………………………………………6分
(2)因为: ,
,
所以: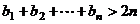 .
………………………………………8分
.
………………………………………8分
又因为: ,
,
所以:
= .
………………………………………11分
.
………………………………………11分
综上,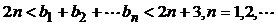 . ……………………………12分
. ……………………………12分
22.解:⑴ 设点M的坐标为(x,y)则由 ,
,
得 ,及
,及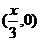
由 得
得 …………………3分
…………………3分
∴ ,由点Q在x轴的正半轴上得
,由点Q在x轴的正半轴上得
∴M点轨迹G方程: (
( )
……………………5分
)
……………………5分
⑵ 设直线 ,其中
,其中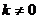 代入
代入
得 (1)
……………………6分
(1)
……………………6分
设A(x1,y1),B(x2,y2),则x1,x2是方程(1)的两个实数
∴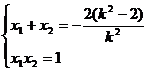 ∴AB中点坐标为
∴AB中点坐标为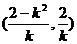
AB的垂直平分线为: ,
……………………8分
,
……………………8分
令 ,
,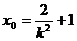 ∴点E的坐标为
∴点E的坐标为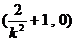
因为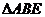 为正三角形
为正三角形
∴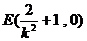 到直线AB的距离等于
到直线AB的距离等于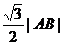 …………………10分
…………………10分
∴ ……12分
……12分
∴ . …………………………………………14分
. …………………………………………14分
