10．
如图所示，在一磁感应强度B=0.5T的匀强磁场中，垂直于磁场方向水平放置着两根相距为L=0.1m的平行金属导轨MN和PQ，导轨电阻忽略不计，在两根导轨的端点N、Q之间连接一阻值R=0.3Ω的电阻．导轨上正交放置着金属棒ab，其电阻r=0.2Ω．当金属棒在水平拉力作用于以速度v=4.0m/s向左做匀速运动时（ ）
如图所示，在一磁感应强度B=0.5T的匀强磁场中，垂直于磁场方向水平放置着两根相距为L=0.1m的平行金属导轨MN和PQ，导轨电阻忽略不计，在两根导轨的端点N、Q之间连接一阻值R=0.3Ω的电阻．导轨上正交放置着金属棒ab，其电阻r=0.2Ω．当金属棒在水平拉力作用于以速度v=4.0m/s向左做匀速运动时（ ）| A． | a b棒所受安培力大小为0.02N | B． | N、Q间电压为0.2V | ||
| C． | a端电势比b端电势低 | D． | 回路中感应电流大小为1A |
9．
如图所示，人用手托着质量为m的苹果，从静止开始以加速度a水平向右做匀加速直线运动，前进距离l后，速度为v，然后以速度v继续向前做匀速直线运动（苹果与手始终相对静止）．已知苹果与手掌之间的动摩擦因数为μ，则下列说法正确的是（ ）
如图所示，人用手托着质量为m的苹果，从静止开始以加速度a水平向右做匀加速直线运动，前进距离l后，速度为v，然后以速度v继续向前做匀速直线运动（苹果与手始终相对静止）．已知苹果与手掌之间的动摩擦因数为μ，则下列说法正确的是（ ）| A． | 苹果一直受到水平向右的摩擦力 | |
| B． | 手对苹果的作用力的方向始终竖直向上 | |
| C． | 在加速阶段手对苹果的作用力等于$\sqrt{（mg）^{2}+（ma）^{2}}$ | |
| D． | 手对苹果做的功为μmgl |
8．
物理学中有些问题的结论不一定必须通过计算才能验证，有时只需通过一定的分析就可以判断结论是否正确．如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环，两圆环上的电荷量均为q（q＞0），而且电荷均匀分布．两圆环的圆心O1和O2相距为2a，联线的中点为O，轴线上的A点在O点右侧与O点相距为r（r＜a）．试分析判断下列关于A点处电场强度大小E的表达式（式中k为静电力常量）正确的是 …（ ）
物理学中有些问题的结论不一定必须通过计算才能验证，有时只需通过一定的分析就可以判断结论是否正确．如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环，两圆环上的电荷量均为q（q＞0），而且电荷均匀分布．两圆环的圆心O1和O2相距为2a，联线的中点为O，轴线上的A点在O点右侧与O点相距为r（r＜a）．试分析判断下列关于A点处电场强度大小E的表达式（式中k为静电力常量）正确的是 …（ ）| A． | E=$|{\frac{{kq{R_1}}}{{[{{R_1}^2+{{（a+r）}^2}}]}}-\frac{{kq{R_2}}}{{[{{R_2}^2+{{（a-r）}^2}}]}}}|$ | |
| B． | E=$|{\frac{{kq{R_1}}}{{[{{R_1}^2+{{（a+r）}^2}}]\frac{3}{2}}}-\frac{{kq{R_2}}}{{[{{R_2}^2+{{（a-r）}^2}}]\frac{3}{2}}}}|$ | |
| C． | E=$|{\frac{kq（a+r）}{{[{{R_1}^2+{{（a+r）}^2}}]}}-\frac{kq（a-r）}{{[{{R_2}^2+{{（a-r）}^2}}]}}}|$ | |
| D． | E=|$\frac{kq（a+r）}{[{{R}_{1}}^{2}+（a+r）^{2}]\frac{3}{2}}$-$\frac{kq（a-r）}{[{{R}_{2}}^{2}+（a-r）^{2}]\frac{3}{2}}$| |
7．下列说法正确的是（ ）
| A． | 不论超重或失重甚至完全失重，物体所受重力是不变的 | |
| B． | 亚里士多德最早提出力不是维持物体运动的原因 | |
| C． | 牛顿通过理想斜面实验得出力不是维持物体运动的原因 | |
| D． | 伽利略利用斜面实验观察得到了物体不受外力时将做匀速直线运动 | |
| E． | 胡克总结出弹簧弹力与形变量间的关系 | |
| F． | 物理学中引入“质点”的模型时，采用了理想化方法 | |
| G． | kg（千克）、N（牛顿）、m（米）都是基本单位 |
6．
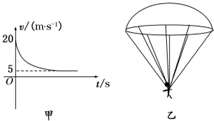某运动员做跳伞训练，他从悬停在空中的直升飞机上由静止跳下，跳离飞机一段时间后打开降落伞做减速下落．他打开降落伞后的速度图线如图甲所示．降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为60°，如图乙．已知人的质量为50kg，降落伞质量也为50kg，不计人所受的阻力，打开伞后伞所受阻力Ff与速度v成正比，即Ff=kv （g取10m/s2）．则（ ）
某运动员做跳伞训练，他从悬停在空中的直升飞机上由静止跳下，跳离飞机一段时间后打开降落伞做减速下落．他打开降落伞后的速度图线如图甲所示．降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为60°，如图乙．已知人的质量为50kg，降落伞质量也为50kg，不计人所受的阻力，打开伞后伞所受阻力Ff与速度v成正比，即Ff=kv （g取10m/s2）．则（ ）| A． | 打开降落伞前人下落的距离为20m | B． | 打开伞瞬间的加速度a=30m/s2 | ||
| C． | 阻力系数k=100 N•s/m | D． | 每根绳承受的拉力至少为200N |
5．如图所示，质量为m的物体A放在倾角为θ=37°的斜面上时，恰好能匀速下滑，现用细线系住物体A，并平行于斜面向上绕过光滑的定滑轮，另一端系住物体B，物体A恰好能沿斜面匀速上滑，（g取10m/s2，sin37°=0.6，cos37°=0.8）则（ ）
| A． | μ=0.75 | B． | μ=0.5 | C． | mB=1.2m | D． | mB=1.6m |
4．甲、乙两小车做直线运动的v-t图象如图所示，由图可知（ ）
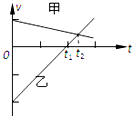
| A． | t1时刻乙车加速度改变方向 | |
| B． | t2时刻两车一定相遇 | |
| C． | 0-t1时间内甲比乙加速度小 | |
| D． | 0-t2时间内乙车一直做单向直线运动 |
3．
如图建筑是厄瓜多尔境内的“赤道纪念碑”．设某人造地球卫星在赤道上空飞行，卫星的轨道平面与地球赤道重合，飞行高度低于地球同步卫星．已知卫星轨道半径为r，飞行方向与地球的自转方向相同，设地球的自转角速度为ω0，地球半径为R，地球表面重力加速度为g，某时刻卫星通过这一赤道纪念碑的正上方，该卫星过多长时间再次经过这个位置？（ ）
如图建筑是厄瓜多尔境内的“赤道纪念碑”．设某人造地球卫星在赤道上空飞行，卫星的轨道平面与地球赤道重合，飞行高度低于地球同步卫星．已知卫星轨道半径为r，飞行方向与地球的自转方向相同，设地球的自转角速度为ω0，地球半径为R，地球表面重力加速度为g，某时刻卫星通过这一赤道纪念碑的正上方，该卫星过多长时间再次经过这个位置？（ ）| A． | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B． | $\frac{2π}{{ω}_{0}+\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C． | $\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | D． | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$-ω0 |
2．
如图甲所示，小物体从竖直轻质弹簧上方离地高h1处由静止释放，其动能Ek与离地高度h的关系如图乙所示，在h1～h2阶段图象为直线，其余部分为曲线，h3对应图象的最高点，小物体的质量为m，重力加速度为g，不计空气阻力，以下说法正确的是（ ）
0 147520 147528 147534 147538 147544 147546 147550 147556 147558 147564 147570 147574 147576 147580 147586 147588 147594 147598 147600 147604 147606 147610 147612 147614 147615 147616 147618 147619 147620 147622 147624 147628 147630 147634 147636 147640 147646 147648 147654 147658 147660 147664 147670 147676 147678 147684 147688 147690 147696 147700 147706 147714 176998
如图甲所示，小物体从竖直轻质弹簧上方离地高h1处由静止释放，其动能Ek与离地高度h的关系如图乙所示，在h1～h2阶段图象为直线，其余部分为曲线，h3对应图象的最高点，小物体的质量为m，重力加速度为g，不计空气阻力，以下说法正确的是（ ）| A． | 弹簧的劲度系数K=$\frac{mg}{{h}_{2}-{h}_{3}}$ | |
| B． | 当物体下落到h=h3高度时，重力势能与弹性势能之和最小 | |
| C． | 小物体处于h=h4高度时，弹簧的弹性势能为Ep=mg（h2-h4） | |
| D． | 在小物体从h1下降到h5过程中，弹簧的最大弹性势能为Epm=mgh1 |