题目内容
3. 如图建筑是厄瓜多尔境内的“赤道纪念碑”.设某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,飞行高度低于地球同步卫星.已知卫星轨道半径为r,飞行方向与地球的自转方向相同,设地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,某时刻卫星通过这一赤道纪念碑的正上方,该卫星过多长时间再次经过这个位置?( )
如图建筑是厄瓜多尔境内的“赤道纪念碑”.设某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,飞行高度低于地球同步卫星.已知卫星轨道半径为r,飞行方向与地球的自转方向相同,设地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,某时刻卫星通过这一赤道纪念碑的正上方,该卫星过多长时间再次经过这个位置?( )| A. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B. | $\frac{2π}{{ω}_{0}+\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C. | $\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | D. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$-ω0 |
分析 在地球表面重力与万有引力大小相等,根据卫星的轨道半径求得卫星的角速度,所以卫星再次经过这个位置需要最短时间为卫星转动比地球转动多一周,从而求得时间
解答 解:在地球表面重力与万有引力相等有:
G$\frac{Mm}{{R}^{2}}$=mg
所以有:GM=gR2
所以卫星的轨道半径r,万有引力提供圆周运动向心力有:
G$\frac{Mm}{{r}^{2}}$=mrω2
可得该卫星的角速度ω=$\sqrt{\frac{GM}{{r}^{3}}}$=$\sqrt{\frac{g{R}^{2}}{{r}^{3}}}$
所以当卫星再次经过该建筑物上空时,卫星比地球多转动一周,所用时间:
t=$\frac{2π}{ω-{ω}_{0}}$
故时间可能为:$\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0}}$或$\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$
故选:C
点评 能根据地面重力与万有引力相等和万有引力提供圆周运动向心力由卫星轨道半径求得卫星的角速度,根据运动关系求时间这是正确解题问题的关键

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
13. 小明去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.小明先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
小明去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.小明先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
 小明去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.小明先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
小明去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.小明先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )| A. | U1一定大于3.0V | B. | U2一定小于9.0V | ||
| C. | U1与U2之和小于12V | D. | U1与U2之比一定不等于1:3 |
14. 如图所示,一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离R处有一小物体与圆盘始终保持相对静止,当小物体从最高点A转到最低点B的过程中,下列关于小物体的说法中正确的是( )
如图所示,一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离R处有一小物体与圆盘始终保持相对静止,当小物体从最高点A转到最低点B的过程中,下列关于小物体的说法中正确的是( )
 如图所示,一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离R处有一小物体与圆盘始终保持相对静止,当小物体从最高点A转到最低点B的过程中,下列关于小物体的说法中正确的是( )
如图所示,一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度ω转动,盘面上离转轴距离R处有一小物体与圆盘始终保持相对静止,当小物体从最高点A转到最低点B的过程中,下列关于小物体的说法中正确的是( )| A. | 所受摩擦力逐渐增大 | B. | 重力的功率逐渐增大 | ||
| C. | 所受的合外力逐渐增大 | D. | 所受摩擦力的方向始终指向圆心 |
11.如图a、b分别是汽车a和b的位置一时间(x-t)图线,则( )


| A. | a做匀速直线运动,b做曲线运动 | |
| B. | 在t1到t2这段时间内,b车的平均速率比a车的大 | |
| C. | 在t1到t2这段时间内,b车的速度一直比a车的大 | |
| D. | 在t1到t2这段时间内,b车的平均速度等于a车的平均速度 |
8.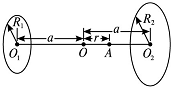 物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是 …( )
物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是 …( )
 物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是 …( )
物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是 …( )| A. | E=$|{\frac{{kq{R_1}}}{{[{{R_1}^2+{{(a+r)}^2}}]}}-\frac{{kq{R_2}}}{{[{{R_2}^2+{{(a-r)}^2}}]}}}|$ | |
| B. | E=$|{\frac{{kq{R_1}}}{{[{{R_1}^2+{{(a+r)}^2}}]\frac{3}{2}}}-\frac{{kq{R_2}}}{{[{{R_2}^2+{{(a-r)}^2}}]\frac{3}{2}}}}|$ | |
| C. | E=$|{\frac{kq(a+r)}{{[{{R_1}^2+{{(a+r)}^2}}]}}-\frac{kq(a-r)}{{[{{R_2}^2+{{(a-r)}^2}}]}}}|$ | |
| D. | E=|$\frac{kq(a+r)}{[{{R}_{1}}^{2}+(a+r)^{2}]\frac{3}{2}}$-$\frac{kq(a-r)}{[{{R}_{2}}^{2}+(a-r)^{2}]\frac{3}{2}}$| |
15.在图中,A、B之间存在摩擦力的有( )
| A. |  A沿粗糙的竖直墙面滑下 | B. | 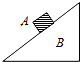 A沿光滑斜面向上运动 | ||
| C. |  A、B一起向右作匀速运动 | D. |  A、B一起向右运动,速度越来越大 |
12.关于重核裂变和轻核聚变,下列说法正确的是( )
| A. | 太阳辐射的能量来自于重核裂变 | |
| B. | 核电站利用聚变反应提供能量 | |
| C. | 核反应堆中的镉棒用于控制链式反应的快慢 | |
| D. | 核聚变的难点是地球聚变燃料匮乏 |
13.质点做直线运动的位移x与时间t的关系为x=t-2t2+5(各物理量采用国际单位制单位),则质点( )
| A. | 第1s内的位移是4m | |
| B. | 前2s内的平均速度大小是1m/s | |
| C. | 任意相邻的1s内位移差大小都是3m | |
| D. | 任意1s内速度的变化量的大小为4m/s |