题目内容
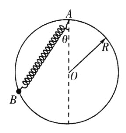
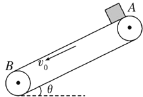
【题目】如图所示,传送带与地面夹角θ=37°,从A到B长度为L=16 m,传送带v0=10 m/s 的速率逆时针转动。在传送带上端A无初速地放一个质量为m=0.5 kg的黑色煤块,它与传送带之间的动摩擦因数为μ=0.5。煤块在传送带上经过会留下黑色痕迹。已知sin 37°=0.6,g=10 m/s2,求:
(1)煤块从A到B的时间;
(2)煤块从A到B的过程中传送带上形成痕迹的长度。
【答案】(1) 2s (2) 5m
【解析】
由题意可知考查传送带模型,根据牛顿第二定律及运动学公式计算可得。
(1) 煤块向下做匀加速运动,由牛顿第二定律可得
![]()
代入数值可得
![]()
设经过时间t1 煤块和传送带速度达到相同
![]()
设下滑距离为x1,由运动学公式
![]()
因为![]() 煤块继续向下加速,由牛顿第二定律可得
煤块继续向下加速,由牛顿第二定律可得
![]()
代入数值可得![]()
设再经过时间t2到达B,下滑距离为x2
![]()
代入数值可求得![]()
![]() (舍去)
(舍去)
![]()
(2) 煤块加速运动时间内传送带运动位移为![]()
![]()
相对运动位移为
![]()
达到共速到煤块加速滑到最低端设传送带运动位移为![]() ,相对滑动位移为
,相对滑动位移为
![]()
相对运动位移为
![]()
考虑到痕迹的重复性,则痕迹的实际长度仍为5m。

练习册系列答案
相关题目
【题目】在“用DIS研究在温度不变时,一定质量的气体压强与体积的关系”实验中,某同学将注射器活塞置于刻度为10mL处,然后将注射器连接压强传感器并开始实验,气体体积V每增加1mL测一次压强p,最后得到p和V的乘积逐渐增大。
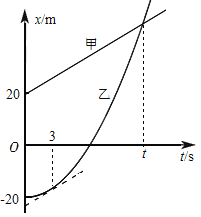
(1)由此可推断,该同学的实验结果可能为图__________。
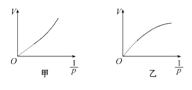
(2)图线弯曲的可能原因是在实验过程中( )
A.注射器中有异物 | B.连接软管中存在气体 |
C.注射器内气体温度升高 | D.注射器内气体温度降低 |