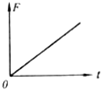题目内容
5. 如图所示,水平桌面上叠放着一质量为m=1kg的金属块A(可看作质点)和质量为M=2kg的木板B,B的长度L=3.5m,A和B之间、B与地面之间的动摩擦因数分别为μ1=0.4,μ2=0.1.现对A施加大小为5N、水平向右的恒力F,同时给B一个瞬时作用使B获得向左的初速度Vo,Vo=3.5m/s,则经过多长时间A从B右端脱离?(g取10m/s2)
如图所示,水平桌面上叠放着一质量为m=1kg的金属块A(可看作质点)和质量为M=2kg的木板B,B的长度L=3.5m,A和B之间、B与地面之间的动摩擦因数分别为μ1=0.4,μ2=0.1.现对A施加大小为5N、水平向右的恒力F,同时给B一个瞬时作用使B获得向左的初速度Vo,Vo=3.5m/s,则经过多长时间A从B右端脱离?(g取10m/s2)
分析 由牛顿第二定律求出A、B的加速度,然后应用匀变速直线运动的速度公式与位移公式求出B向左做匀减速直线运动的时间与位移,然后求出B向右做匀加速直线运动的加速度,再应用匀变速直线运动的位移公式求出A向右运动到脱离B的时间,最后求出总的运动时间.
解答 解:B向左运动过程中,由牛顿第二定律,
对A:F-μ1mg=maA
对B:μ1mg+μ2(M+m)g=M aB
解得:aA=1m/s2,aB=3.5m/s2,
设经时间t1,B速度减为零:t1=$\frac{{v}_{0}}{{a}_{B}}$=1s,
A的位移:x1=$\frac{1}{2}$aAt12=0.5m,向右,
B的位移:x2=$\frac{1}{2}$vot1=1.75m,向左,
此时A离B右端:d=L-(x1+x2)=1.25m,
B反向向右加速:aB′=$\frac{{{u_1}mg-{u_2}(M+m)g}}{M}$=0.5m/s2,
设经时间t2A到达B的右端:d=aA t1 t2+$\frac{1}{2}$aB t22-$\frac{1}{2}$aB′t22,
解得:t2=1s(另一解为负,舍去),总时间t=t1+t2=2s;
答:经过2sA从B右端脱离.
点评 本题考查了A的运动时间,考查了牛顿第二定律与运动学公式的应用,分析清楚物体的运动过程是解题的关键,应用牛顿第二定律与运动学公式可以解题.

练习册系列答案
相关题目
4. 如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T=0.02s,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A,那么( )
如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T=0.02s,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A,那么( )
 如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T=0.02s,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A,那么( )
如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T=0.02s,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A,那么( )| A. | 线圈中感应电流的有效值为2A | |
| B. | 线圈消耗的电功率为8W | |
| C. | 任意时刻线圈中的感应电动势为e=4cos100πtV | |
| D. | 任意时刻穿过线圈的磁通量为Φ=$\frac{0.02}{π}$sin100πtWb |
5.下列说法中正确的是( )
| A. | 在${\;}_1^2H+{\;}_1^3H→{\;}_2^4{H_e}+x$核反应中,x是质子,核反应放出的能量等于${\;}_1^2H$和${\;}_1^3H$的质量和减去${\;}_2^4{H_e}$和x的质量和,再乘c2(c表示光速) | |
| B. | 卫星可以在大于地球半径的任意圆轨道上运动,电子也可以在大于基态轨道半径的任意圆轨道上运动 | |
| C. | 分别用绿光和紫光照射同一金属表面都能发生光电效应,逸出的光电子的动能可能相等 | |
| D. | 随着温度的升高,一方面各种波长的辐射强度都有增加,另一方面辐射强度的极大值向波长较短的方向移动 | |
| E. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此光子散射后波长变长 | |
| F. | 在α粒子散射实验中,当在α粒子最接近原子核时,α粒子与金原子核组成的系统能量最小 |
2. 如图所示,一个质点做圆周运动,A、B、C是其轨迹上的三点.下列说法正确的是( )
如图所示,一个质点做圆周运动,A、B、C是其轨迹上的三点.下列说法正确的是( )
 如图所示,一个质点做圆周运动,A、B、C是其轨迹上的三点.下列说法正确的是( )
如图所示,一个质点做圆周运动,A、B、C是其轨迹上的三点.下列说法正确的是( )| A. | 质点A可能做匀速运动 | |
| B. | 质点一定做变速运动 | |
| C. | 质点受到的合力可能等于零 | |
| D. | 质点经过A、C两点时的速度可能相同 |
9.真空中有两个等量异种点电荷,它们连线中点的场强大小为E.那么在这两个点电荷的连线上,与其中一个点电荷的距离等于两点电荷连线长度的$\frac{1}{4}$的点处,其场强大小为( )
| A. | $\frac{4}{3}$E | B. | 2E | C. | $\frac{20}{9}$E | D. | $\frac{20}{3}$E |
10.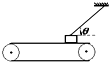 如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L,稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时(v1<v2),绳中的拉力分别为Fl、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为tl、t2,达到左端速度分别为v′1、v′2.则下列说法正确的是( )
如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L,稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时(v1<v2),绳中的拉力分别为Fl、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为tl、t2,达到左端速度分别为v′1、v′2.则下列说法正确的是( )
 如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L,稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时(v1<v2),绳中的拉力分别为Fl、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为tl、t2,达到左端速度分别为v′1、v′2.则下列说法正确的是( )
如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L,稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时(v1<v2),绳中的拉力分别为Fl、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为tl、t2,达到左端速度分别为v′1、v′2.则下列说法正确的是( )| A. | F1=F2 | B. | Fl<F2 | C. | v′1=v′2 | D. | tl>t2 |
17. 如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )
如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )
 如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )
如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )| A. | F一直减小 | B. | F先增大后减小 | C. | FN一直增大 | D. | FN先减小后不变 |
15.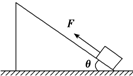 如图所示,一质量为m的物体静置在倾角为30°的光滑斜面底端.现用沿斜面向上的恒力F拉物体,使其做匀加速直线运动,经时间t,力F做功为W,此后撤去恒力F,物体又经时间t回到出发点,若以斜面底端为重力势能零势能面,则下列说法正确的是( )
如图所示,一质量为m的物体静置在倾角为30°的光滑斜面底端.现用沿斜面向上的恒力F拉物体,使其做匀加速直线运动,经时间t,力F做功为W,此后撤去恒力F,物体又经时间t回到出发点,若以斜面底端为重力势能零势能面,则下列说法正确的是( )
 如图所示,一质量为m的物体静置在倾角为30°的光滑斜面底端.现用沿斜面向上的恒力F拉物体,使其做匀加速直线运动,经时间t,力F做功为W,此后撤去恒力F,物体又经时间t回到出发点,若以斜面底端为重力势能零势能面,则下列说法正确的是( )
如图所示,一质量为m的物体静置在倾角为30°的光滑斜面底端.现用沿斜面向上的恒力F拉物体,使其做匀加速直线运动,经时间t,力F做功为W,此后撤去恒力F,物体又经时间t回到出发点,若以斜面底端为重力势能零势能面,则下列说法正确的是( )| A. | 恒力F大小为mg | |
| B. | 从开始到回到出发点的整个过程中机械能增加了W | |
| C. | 回到出发点时重力的瞬时功率为g$\sqrt{2Wm}$ | |
| D. | 物体动能与势能相等的位置在撤去恒力位置的上方 |
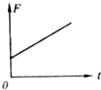
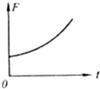
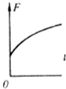
 如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( )
如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( )