题目内容
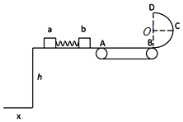
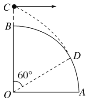
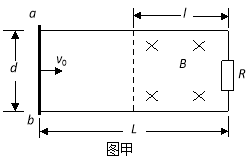
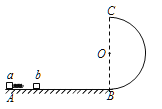
【题目】如图所示,水平光滑轨道AB与半径为R的竖直光滑半圆形轨道BC相切于B点。质量为2m和m的a、b两个小滑块(可视为质点)原来静止于水平轨道上,其中小滑块a与一轻弹簧相连。某一瞬间给小滑块a一冲量使其获得![]() 的初速度向右冲向小滑块b,与b碰撞后弹簧不与b相粘连,且小滑块b在到达B点之前已经和弹簧分离,不计一切摩擦,求:
的初速度向右冲向小滑块b,与b碰撞后弹簧不与b相粘连,且小滑块b在到达B点之前已经和弹簧分离,不计一切摩擦,求:
(1)a和b在碰撞过程中弹簧获得的最大弹性势能;
(2)小滑块b与弹簧分离时的速度;
(3)试通过计算说明小滑块b能否到达圆形轨道的最高点C。若能,求出到达C点的速度;若不能,求出滑块离开圆轨道的位置和圆心的连线与水平方向的夹角![]() 。(求出
。(求出![]() 角的任意三角函数值即可)。
角的任意三角函数值即可)。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)a与b碰撞达到共速时弹簧被压缩至最短,弹性势能最大。设此时ab的速度为v,则由系统的动量守恒可得
2mv0=3mv
由机械能守恒定律
![]()
解得:![]()
(2)当弹簧恢复原长时弹性势能为零,b开始离开弹簧,此时b的速度达到最大值,并以此速度在水平轨道上向前匀速运动。设此时a、b的速度分别为v1和v2,由动量守恒定律和机械能守恒定律可得:
2mv0=2mv1+mv2
![]()
解得: ![]()
(3)设b恰能到达最高点C点,且在C点速度为vC,
由牛顿第二定律: ![]()
解得:![]()
再假设b能够到达最高点C点,且在C点速度为vC',由机械能守恒定律可得:
![]()
解得vC'=0<![]() 。所以b不可能到达C点
。所以b不可能到达C点
假设刚好到达与圆心等高处,由机械能守恒![]()
解得![]() <
<![]() 所以能越过与圆心等高处
所以能越过与圆心等高处
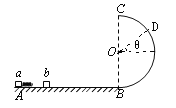
设到达D点时离开,如图设倾角为![]() :刚好离开有N=0,由牛顿第二定律:
:刚好离开有N=0,由牛顿第二定律:
![]()
从B到D有机械能守恒有:![]()
解得:![]()

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目