题目内容
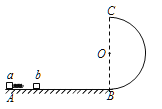
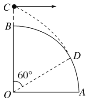
【题目】如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°,则C点到B点的距离为( )
A. R B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由几何知识求解水平射程.根据平抛运动的速度与水平方向夹角的正切值得到初速度与小球通过D点时竖直分速度的关系,再由水平和竖直两个方向分位移公式列式,求出竖直方向上的位移,即可得到C点到B点的距离。
设小球平抛运动的初速度为v0,将小球在D点的速度沿竖直方向和水平方向分解,则有![]() ,解得:
,解得:![]() ,小球平抛运动的水平位移:x=Rsin 60°,x=v0t,解得:
,小球平抛运动的水平位移:x=Rsin 60°,x=v0t,解得:![]() ,
,![]() ,设平抛运动的竖直位移为y,
,设平抛运动的竖直位移为y,![]() ,解得:
,解得:![]() ,则BC=y-(R-Rcos 60°)=
,则BC=y-(R-Rcos 60°)=![]() ,故D正确,ABC错误。
,故D正确,ABC错误。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目