题目内容
【题目】如图所示，在水平向左的匀强电场中，一带电小球质量为m,电量为-q。用绝缘轻绳(不伸缩)悬于O点，平衡时小球位于A点，此时绳与竖直方向的夹角θ＝30°。绳长为l，AO＝CO＝DO＝l，OD水平，OC竖直。求：
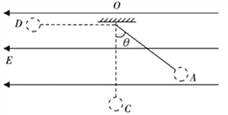
(1)电场强度E；
(2)把小球移到D点后，让小球由静止自由释放，小球向右摆动到Ａ点时的速率和该时刻轻绳中张力(计算结
果可带根号)。
【答案】（1）
（2）
； 
【解析】试题分析：（1）小球在A点处于平衡状态：
电场强度
（2）当小球移到D点后，让小球由静止自由释放，小球先沿电场力与重力的合力的方向做匀加速直线运动，由D运动到B， OB与竖直方向夹角为30°方向绳绷直，A、B关于OC对称，设此时速度为vB。
根据牛顿第二定律：
解得小球的加速度
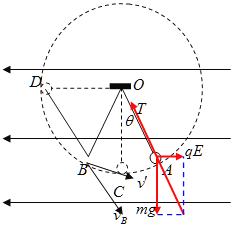
根据几何关系可知，由D到B位移等于绳长l，根据
解得：小球刚运动到B时的速度
绳绷直后，小球沿绳方向的分速度变为零，垂直绳方向速度
不变，使小球绕O点做圆周运动
小球从B点做圆周运动的速度
小球运动到A点切向加速度为零，圆周运动的速度达到最大
由B到A位移为l，重力做功为零，根据动能定理，有：
解得：小球运动到A时的速度
所以，小球向右摆动过程中的运动到A点时有最大速率，最大速率
根据牛顿第二定律，有
此时轻绳中张力
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
