题目内容
6.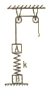 如图所示,物体A经一轻质弹簧与下方地面上物体B相连,弹簧的劲度系数为k,A、B质量均为m且都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,现在挂钩上挂一质量为m的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将物体C换成另一个质量为2m的物体D,仍从上述初始位置由静止状态释放,则这次物体B刚离地时,物体A的( )
如图所示,物体A经一轻质弹簧与下方地面上物体B相连,弹簧的劲度系数为k,A、B质量均为m且都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,现在挂钩上挂一质量为m的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将物体C换成另一个质量为2m的物体D,仍从上述初始位置由静止状态释放,则这次物体B刚离地时,物体A的( )| A. | 加速度为零 | B. | 加速度为$\frac{1}{3}$g | C. | 动能为$\frac{{m}^{2}{g}^{2}}{3k}$ | D. | 动能为$\frac{2{m}^{2}{g}^{2}}{3k}$ |
分析 对B受力分析,物体B刚离地时,重力和弹簧弹力相等,由牛顿第二定律求解加速度,再对A分析确定B离地时,A上升的高度,利用机械能守恒求解A的动能.
解答 解:A、B、开始时B受重力和地面支持力,随着C的运动又受到弹簧弹力,物体B刚离地时,支持力为零,重力和弹簧弹力相等,根据牛顿第二定律可知此时的加速度为零,故A正确;B错误;
C、D、开始时,A、B静止,设弹簧压缩量为x1,对A有:kx1=mg
挂C并释放后,C向下运动,A向上运动,设B刚要离地时弹簧伸长量为x2,对B有:kx2=mg
C下落的高度h等于A上升的高度,$h={x}_{1}+{x}_{2}=\frac{2mg}{k}$
ABC组成系统在运功过程中只有重力和弹簧弹力做功,系统机械能守恒,即开始的弹簧的弹性势能和C减小的重力势能转化为弹簧的弹性势能和A增加的势能及AC的动能,又因x1=x2,则开始的弹性势能与后来的弹性势能相等,故${{E}_{P前}+m}_{C}gh={{E}_{P后}+m}_{A}gh+\frac{1}{2}{m}_{A}{v}^{2}+\frac{1}{2}{m}_{C}{v}^{2}$,即:2mgh=mgh$+\frac{1}{2}3m{v}^{2}$,解得:$\frac{1}{2}m{v}^{2}=\frac{1}{3}mgh=\frac{2{m}^{2}{g}^{2}}{3k}$,故C错误;D正确;
故选:AD
点评 本题关键分析清楚物体的运动规律,注意开始时弹簧被压缩,后来被拉伸,变化量为两者之和,然后根据平衡条件和机械能守恒定律以及胡克定律列式后联立求解即可,

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | F与r2成反比 | B. | F与r2成正比 | C. | F与r3成正比 | D. | F与r4成正比 |
| A. | 根据加速度的定义a=$\frac{△v}{△t}$,当△t非常小,$\frac{△v}{△t}$就可以表示物体在t时刻的瞬时加速度 | |
| B. | 在探究加速度、力和质量三者之间关系时,先保持质量不变,研究加速度与力的关系,再保持力不变,研究加速度与质量的关系 | |
| C. | 在推导匀变速直线运动的位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加 | |
| D. | 在不需要考虑物体本身的大小和形状时,用点来代替物体,即质点 |
| A. | 地球同步卫星的运行周期为24小时 | |
| B. | 地球同步卫星可以在地面上任一点的正上方,但离地心的距离是一定的 | |
| C. | 地球同步卫星只能在赤道的正上方,但离地心的距离可按需要选择不同的值 | |
| D. | 以上说法均不正确 |
| A. | “神舟星”的线速度大 | B. | “神舟星”的周期大 | ||
| C. | “神舟星”的轨道半径大 | D. | 不能确定 |
 如图所示,Q是放在绝缘柄上的带正电的物体,把一个系在绝缘丝线上的带正电的小球,先后挂在图中的A、B两个位置,小球两次平衡时,丝线偏离竖直方向的夹角分别为θ1、θ2,则θ1和θ2的关系是( )
如图所示,Q是放在绝缘柄上的带正电的物体,把一个系在绝缘丝线上的带正电的小球,先后挂在图中的A、B两个位置,小球两次平衡时,丝线偏离竖直方向的夹角分别为θ1、θ2,则θ1和θ2的关系是( )| A. | θ1<θ2 | B. | θ1=θ2 | C. | θ1>θ2 | D. | 无法确定 |
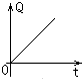
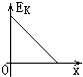
 如图所示,质量为m的滑块以一定初速度滑上倾角为θ的固定斜面,同时施加一沿斜面向上的恒力F=mgsinθ;已知滑块与斜面间的动摩擦因数μ=tanθ,取出发点为参考点,能正确描述滑块运动到最高点过程中产生的热量Q?滑块重力势能EP随时间t的关系及动能Ek?机械能E随位移x的关系的是:( )
如图所示,质量为m的滑块以一定初速度滑上倾角为θ的固定斜面,同时施加一沿斜面向上的恒力F=mgsinθ;已知滑块与斜面间的动摩擦因数μ=tanθ,取出发点为参考点,能正确描述滑块运动到最高点过程中产生的热量Q?滑块重力势能EP随时间t的关系及动能Ek?机械能E随位移x的关系的是:( )