Question

【题目】如图所示，在水平桌面上A点处静止有一辆可视为质点、质量为m=0.2kg的电动小车，以恒定的功率 P=3W启动并向右运动，当速度为 v1=2m/s时加速度为a1=2.5m/s2。小车运动到水平桌面的右侧边缘B点时刚好加速到最大速度，而后关闭电动小车的电源，小车从B点飞出，沿切线方向从C点进入固定的光滑圆弧轨道CDEF，并沿轨道恰好通过最高点F。已知FOD竖直，COE为圆弧的一条直径，圆弧CD的圆心角θ=53°，重力加速度g=10m/s2，sin53°=0.8，cos53°=0.6。求：

（1）小车在水平桌面上运动过程中受到的阻力大小f；

（2）小车在 B点的速度大小vm；

（3）平台末端 B点到 C点的竖直高度H；

（4）现将半圆槽上半部的 EF部分去掉，小滑块从E点脱离半圆槽后继续上升离E点的最大高度h。

Answer 1

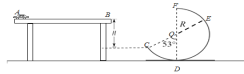
【答案】（1）1.0N；（2）3m/s；（3）0.8m；（4）m；

【解析】

(1) 设小车在水平桌面上受到的阻力大小为f，当小车速度为v1=2m/s时，

牵引力为F1，则P=F1v1

F1-f=ma1

解得f=1.0N；

(2) 设小车在B点时，小车的牵引力为F2 ,A、B两点间的距离为x，则

P=F2vm

F2=f

解得vm=3m/s

(3) 在C点进行速度的分解有

所以

(4) 设小车在C点时的速度大小设为vC

解得：

恰好运动到F点，有中力提供偏向力，即

从C到F由机械能守恒定律有

从C到E由机械能守恒定律有

则离开半圆槽时的速度：

其竖直分速度：

由公式

解得：。