Question

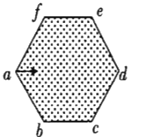
【题目】宇宙中存在一些离其他恒星较远的四颗星组成的系统，通常可忽略其他星体对它们的引力作用。天眼在观察中发现三颗质量均为m的星球A、B、C恰构成一个边长为L的正三角形，在它们的中心O处还有一颗质量为3m的星球，如图所示。已知引力常量为G，四个星球的密度相同，每个星球的半径均远小于L。对于此系统，若忽略星球自转，则下列说法正确的是（　　）

A.A、B、C三颗星球的线速度大小均为

B.A、B、C三颗星球的加速度大小均为

C.星球A和中心O处的星球表面的重力加速度之比为1∶2

D.若O处的星球被均分到A、B、C三颗星球上，A、B、C三颗星球仍按原轨道运动，则A、B、C三颗星球运动的周期将变大

Answer 1

【答案】AD

【解析】

AB．对三绕一模式，等边三角形边长为，三颗绕行星轨道半径均为，由几何关系得三角形的边长为

即有

对顶点的星体受力分析，根据矢量合成的方法可得

解得

，

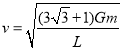故A正确，B错误；

C．设它们的密度为，半径为，则有

表面的重力加速度

联立可得

同理可得处的星球表面的重力加速度

所以它们表面的重力加速度的比值为

故C错误；

D．由可得

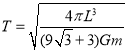
若处的星球被均分到、、三颗星球上，、、三颗星球的质量都是；若仍按原轨道运动，则对有

可得

则、、三颗星球运动的周期将变大，故D正确。

故选AD。