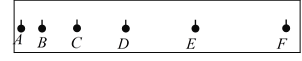题目内容
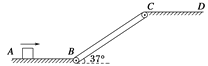
【题目】如图所示,AB、CD为两个光滑的平台,一倾角为37°、长为5 m的传送带与两平台平滑连接。现有一小物体以10 m/s的速度沿平台AB向右运动,当传送带静止时,小物体恰好能滑到平台CD上。(g取10 m/s2,sin37°=0.6,cos37°=0.8)
(1)求小物体跟传送带间的动摩擦因数;
(2)当小物体在平台AB上的运动速度低于某一数值时,无论传送带顺时针运动的速度有多大,小物体都不能到达平台CD,求这个临界速度;
(3)若小物体以8 m/s的速度沿平台AB向右运动,欲使小物体能到达平台CD,传送带至少以多大的速度顺时针运动?
【答案】(1)0.5(2)2![]() m/s;(3)3m/s
m/s;(3)3m/s
【解析】
(1)传送带静止时,小物体在传送带上受力如图甲所示,
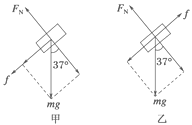
根据牛顿第二定律得:
μmgcos37°+mgsin37°=ma1
B→C过程,有:
v02=2a1l
解得:
a1=10 m/s2,μ=0.5。
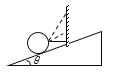
(2)当小物体在传送带上受到的摩擦力始终向上时,最容易到达传送带顶端,此时,小物体受力如图乙所示,根据牛顿第二定律得:
mgsin37°-μmgcos37°=ma2
若恰好能到达平台CD,有:
v2=2a2l
解得:
v=2![]() m/s,a2=2 m/s2
m/s,a2=2 m/s2
即当小物体在平台AB上向右运动的速度小于2![]() m/s时,无论传送带顺时针运动的速度有多大,小物体都不能到达平台CD。
m/s时,无论传送带顺时针运动的速度有多大,小物体都不能到达平台CD。
(3)设小物体在平台AB上的运动速度为v1,传送带顺时针运动的速度大小为v2。
从小物体滑上传送带至小物体速度减小到传送带速度过程,有:
v12-v22=2a1x1
从小物体速度减小到传送带速度至恰好到达平台CD过程,有:
v22=2a2x2,
x1+x2=l
解得:
v2=3 m/s,
即传送带至少以3 m/s的速度顺时针运动,小物体才能到达平台CD。

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】小华同学在做“用打点计时器测速度”的实验时,从打下的若干纸带中选出了如图1所示的一条纸带,已知打点计时器使用的电源频率为50Hz,每两个相邻计数点间有四个点没有画出,各计数点到0点的距离如纸带上所示.
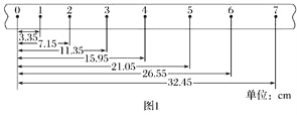

(1)为了达到实验的目的,除了有打点计时器、纸带、小车、细绳、导线、低压交流电源、小木块、长木板外,还需要的仪器有___
A.刻度尺 B.铁架台 C.停表 D.天平
(2)图中两计数点的时间间隔为T=_________s.
(3)根据纸带提供的信息,小华同学已经计算出了打下1、2、3、4、6这五个计数点时小车的速度,请你帮助他计算出打下计数点5时小车的速度v5=__________m/s(结果保留3位有效数字),并填入表中.
计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 0.358 | 0.400 | 0.440 | 0.485 | 0.570 |
(4)以速度v为纵轴、时间t为横轴在图2坐标纸上建立直角坐标系,根据表中的v、t数据,在坐标系中描点,并作出小车运动的v﹣t图象.
(________)
(5)根据v﹣t图象可知,小车运动的加速度大小为_______________m/s2(结果保留3位有效数字).