题目内容
如图所示,足够长的平行金属导轨MN、PQ平行放置,间距为L,与水平面成θ角,导轨与固定电阻R1和R2相连,且R1=R2=R.R1支路串联开关S,原来S闭合,匀强磁场垂直导轨平面斜向上.有一质量为m的导体棒ab与导轨垂直放置,接触面粗糙且始终接触良好,导体棒的有效电阻也为R.现让导体棒从静止释放沿导轨下滑,当导体棒运动达到稳定状态时速率为v,此时整个电路消耗的电功率为重力功率的3/4.重力加速度为g,导轨电阻不计.试求:

(1)在上述稳定状态时,导体棒中的电流I,以及磁感应强度B的大小;
(2)当断开开关S后,导体棒ab所能达到的最大速率v′是v的多少倍?
(1)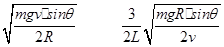
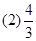
【解析】(1)当导体棒以速率v匀速下降时,电路中的总电阻R总=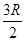 ①
①
感应电动势 E=BLv ②
导体棒中的电流I=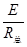 ③
③
总电功率 P电=I2R总 ④
重力功率 P重=mgv·sinθ ⑤
根据题意有
P电=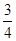 P重 ⑥
P重 ⑥
由①②③④⑤⑥解得: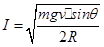 ⑦
⑦
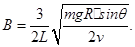 ⑧
⑧
(2)由S断开前的情况可知:
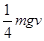 ·sinθ=μmgv·cosθ ⑨
·sinθ=μmgv·cosθ ⑨
S断开后,当导体棒以速度v′匀速下滑时
总电阻 R′总=2R ⑩
导体棒中的电流 I′=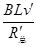 ? (11)?
? (11)?
由导体棒受力平衡有 mgsinθ=μmgcosθ+BI′L? (12)?
由⑧⑨⑩(11)(12)求得: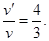

 如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞导热性能良好,其间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,水银深H=10cm,气柱长L=20cm,大气压强p0=75cmHg.现使活塞B缓慢上移,直到A活塞上移H/2的距离,气体温度不变.则对于被封气体:
如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞导热性能良好,其间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,水银深H=10cm,气柱长L=20cm,大气压强p0=75cmHg.现使活塞B缓慢上移,直到A活塞上移H/2的距离,气体温度不变.则对于被封气体: 如图所示,MN为平行板电容器C两极板,虚线到两极板距离相等,极板长为L,两极板的间距为d.右端为屏,屏足够大与极板垂直,到极板的距离为D,有一细电子束沿图中虚线以速度v0连续不断地射入电场且能穿出.已知电子电量为e,电子质量为m,平行板电容器极板间可调偏转电压为U,忽略细电子束的宽度及电子所受的重力及电子间的相互作用力.求:
如图所示,MN为平行板电容器C两极板,虚线到两极板距离相等,极板长为L,两极板的间距为d.右端为屏,屏足够大与极板垂直,到极板的距离为D,有一细电子束沿图中虚线以速度v0连续不断地射入电场且能穿出.已知电子电量为e,电子质量为m,平行板电容器极板间可调偏转电压为U,忽略细电子束的宽度及电子所受的重力及电子间的相互作用力.求: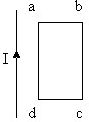 矩形线圈abcd位于足够长的通电直导线附近,且线圈平面与导线在同一平面内,如图所示,线圈的两条边ad和bc与导线平行,要使线圈中产生abcda方向的电流,可以( )
矩形线圈abcd位于足够长的通电直导线附近,且线圈平面与导线在同一平面内,如图所示,线圈的两条边ad和bc与导线平行,要使线圈中产生abcda方向的电流,可以( )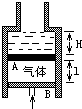 (2011?崇明县二模)如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,当时气体温度为23℃水银深H=10cm,气柱长L=20cm,大气压强p0=75cm Hg.现保持温度不变,使活塞B缓慢上移,直到水银的一半被推入细筒中,
(2011?崇明县二模)如图所示,固定的竖直圆筒由上段细筒和下段粗筒组成,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质光滑活塞间封有空气,活塞A上方有水银.用外力向上托住活塞B,使之处于静止状态,活塞A上方的水银面与粗筒上端相平,当时气体温度为23℃水银深H=10cm,气柱长L=20cm,大气压强p0=75cm Hg.现保持温度不变,使活塞B缓慢上移,直到水银的一半被推入细筒中, 如图所示,MN为平行板电容器C两极板,极板长为L,两极板的间距为d,虚线到M板距离为
如图所示,MN为平行板电容器C两极板,极板长为L,两极板的间距为d,虚线到M板距离为