题目内容
 如图所示,MN为平行板电容器C两极板,极板长为L,两极板的间距为d,虚线到M板距离为
如图所示,MN为平行板电容器C两极板,极板长为L,两极板的间距为d,虚线到M板距离为| 1 | 3 |
(1)两板间所加偏转电压UMN的范围
(2)若两板间电压恒定为U0,且N板电势比M板高,电子飞出平行板时的动能多大?
(3)在(2)这种情况下,电子到达屏上时,它离O点的距离y.
分析:(1)电子在偏转电场中做类平抛运动,根据牛顿第二定律和运动学公式求出偏转位移,结合偏转位移的范围求出两板间所加偏转电压UMN的范围.
(2)根据偏转电压,得出偏转位移的大小,通过动能定理求出电子飞出平行板时的动能大小.
(3)粒子飞出偏转电场时,速度的反向延长线经过轴线的中点,通过相似三角形求出电子到达屏上时离O点的距离.
(2)根据偏转电压,得出偏转位移的大小,通过动能定理求出电子飞出平行板时的动能大小.
(3)粒子飞出偏转电场时,速度的反向延长线经过轴线的中点,通过相似三角形求出电子到达屏上时离O点的距离.
解答: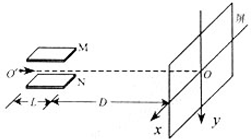 解 (1)电子在电场中做类平抛运动
解 (1)电子在电场中做类平抛运动
垂直电场方向 有L=v0t
沿电场方向 有y=
at2
其中 a=
,F=eE,E=
,a=
则y=
当-
<y<
时,电子能从极板间穿出
所以 -
<U<
.
(2)当两板电压恒定为U0时,则y=
由动能定理得:eEy=
mv2-
m
所以飞出极板时的动能为Ek=
mv2=
m
+
.
(3)由相似三角形得
=
y′=
y=(2D+L)
.
答:(1)两板间所加偏转电压UMN的范围-
<U<
.
(2)电子飞出平行板时的动能为Ek=
m
+
.
(3)电子到达屏上时,它离O点的距离为y′=(2D+L)
.
 解 (1)电子在电场中做类平抛运动
解 (1)电子在电场中做类平抛运动垂直电场方向 有L=v0t
沿电场方向 有y=
| 1 |
| 2 |
其中 a=
| F |
| m |
| U |
| d |
| eU |
| md |
则y=
| eUL2 | ||
2md
|
当-
| d |
| 3 |
| 2d |
| 3 |
所以 -
2md2
| ||
| 3eL2 |
4md2
| ||
| 3eL2 |
(2)当两板电压恒定为U0时,则y=
| eU0L2 | ||
2md
|
由动能定理得:eEy=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
所以飞出极板时的动能为Ek=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
e2
| ||
2md2
|
(3)由相似三角形得
| y′ |
| y |
D+
| ||
|
y′=
D+
| ||
|
| eU0L | ||
2md
|
答:(1)两板间所加偏转电压UMN的范围-
2md2
| ||
| 3eL2 |
4md2
| ||
| 3eL2 |
(2)电子飞出平行板时的动能为Ek=
| 1 |
| 2 |
| v | 2 0 |
e2
| ||
2md2
|
(3)电子到达屏上时,它离O点的距离为y′=(2D+L)
| eU0L | ||
2md
|
点评:会用运动的合成与分解处理类平抛运动问题,根据物体运动的受力情况,确定粒子运动性质,确定物体运动的轨迹并能根据几何关系求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?厦门一模)如图所示,MN为两平行金属板,O、O为两金属板中心处正对的两个小孔,N板的右侧空间有磁感应强度大小均为B且方向相反的两匀强磁场区,图中N板与虚线CD、PQ为两磁场边界线,三条界线平行,两磁场区域的宽度分别为d和3d,沿边界线方向磁场区域足够大.在两金属板上加上大小可调节的直流电压,质量为m、电量为-q的带电粒子(重力不计);从O点由静止释放,经过MN板间的电场加速后,从O'沿垂直于磁场方向射入磁场,若粒子能穿过CD界并进入CD右侧磁场但不能穿过PQ界,最终打到N板而结束运动,试求:
(2013?厦门一模)如图所示,MN为两平行金属板,O、O为两金属板中心处正对的两个小孔,N板的右侧空间有磁感应强度大小均为B且方向相反的两匀强磁场区,图中N板与虚线CD、PQ为两磁场边界线,三条界线平行,两磁场区域的宽度分别为d和3d,沿边界线方向磁场区域足够大.在两金属板上加上大小可调节的直流电压,质量为m、电量为-q的带电粒子(重力不计);从O点由静止释放,经过MN板间的电场加速后,从O'沿垂直于磁场方向射入磁场,若粒子能穿过CD界并进入CD右侧磁场但不能穿过PQ界,最终打到N板而结束运动,试求: 如图所示,MN为通有稳恒电流I1的长直导线,位于MN右侧的ABCD为通有电流I2=10A的矩形线圈,共有10匝,已知AB=12cm,BC=20cm,AD与BC都平行于MN,与MN都相距10cm,线圈能绕过AB及CD中点的轴转动,此时线圈所受磁场力的力矩为2.4×10-3N?m,则从上向下俯视,该力矩为
如图所示,MN为通有稳恒电流I1的长直导线,位于MN右侧的ABCD为通有电流I2=10A的矩形线圈,共有10匝,已知AB=12cm,BC=20cm,AD与BC都平行于MN,与MN都相距10cm,线圈能绕过AB及CD中点的轴转动,此时线圈所受磁场力的力矩为2.4×10-3N?m,则从上向下俯视,该力矩为 如图所示,MN为正对的两个平行板,可以吸附打到板上的电子,两板间距离为d,板长为7d.在两个平行板间只有方向垂直于纸面向里的匀强磁场.若有电量为e的电子流,从左侧不同位置进入两板间的虚线框区域,已知电子的动量大小为p,方向平行于板.为了使进入两板间的电子都能打到两板上,被两板吸收,磁场的磁感应强度大小取值可能是下述四个值中的
如图所示,MN为正对的两个平行板,可以吸附打到板上的电子,两板间距离为d,板长为7d.在两个平行板间只有方向垂直于纸面向里的匀强磁场.若有电量为e的电子流,从左侧不同位置进入两板间的虚线框区域,已知电子的动量大小为p,方向平行于板.为了使进入两板间的电子都能打到两板上,被两板吸收,磁场的磁感应强度大小取值可能是下述四个值中的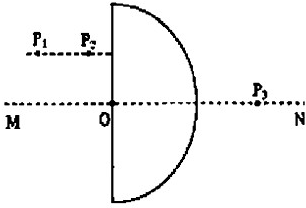 如图所示,MN为半圆形玻璃砖的对称轴,O为玻璃砖圆心,某同学在与MN平行的直线上插上两根大头针P1、P2,在MN上插大头钱P3,从P3一侧透过玻璃砖观察P1、P2的像,调整P3位置使P3能同时挡住P1、P2的像,确定了的P3位置如图所示,他测得玻璃砖直径D=8cm,P1P2连线与MN之间的距离d1=2cm,P3到O的距离d2=6.92cm.
如图所示,MN为半圆形玻璃砖的对称轴,O为玻璃砖圆心,某同学在与MN平行的直线上插上两根大头针P1、P2,在MN上插大头钱P3,从P3一侧透过玻璃砖观察P1、P2的像,调整P3位置使P3能同时挡住P1、P2的像,确定了的P3位置如图所示,他测得玻璃砖直径D=8cm,P1P2连线与MN之间的距离d1=2cm,P3到O的距离d2=6.92cm.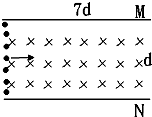 如图所示,MN为正对的两个平行板,可以吸附打到板上的电子,两板间距距离为d,板长为7d在两个平行板间只有方向垂直于纸面向里的匀强磁场.若有电量为e的电子流,从左侧不同位置进入两板间的虚线框中,已知电子的动量大小为p,方向平行于板.为了使进入两板间的电子都能打到两板上,被两板接收,磁场的磁感应强度大小取值可能是下述四个值中的( )
如图所示,MN为正对的两个平行板,可以吸附打到板上的电子,两板间距距离为d,板长为7d在两个平行板间只有方向垂直于纸面向里的匀强磁场.若有电量为e的电子流,从左侧不同位置进入两板间的虚线框中,已知电子的动量大小为p,方向平行于板.为了使进入两板间的电子都能打到两板上,被两板接收,磁场的磁感应强度大小取值可能是下述四个值中的( )