题目内容
(19分)一个质量m =0.1kg的正方形金属框,其电阻R=0.5Ω,金属框放在表面绝缘且光滑的斜面顶端(金属框上边与AB重合),由静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边CD平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与CD重合)。设金属框在下滑过程中的速度为v,与此对应的位移为s, 那么v2-s图像如图所示,已知匀强磁场方向垂直斜面向上,取g=10m/s2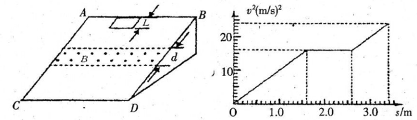
(1)根据v2-s图像所提供的信息,计算斜面的倾角θ和匀强磁场的宽度d
(2)计算匀强磁场的磁感应强度B的大小;
(3)现用平行于斜面沿斜面向上的恒力F1作用在金属框上,使金属框从斜面底端CD(金属 框下边与CD重合)由静止开始沿斜面向上运动,匀速通过磁场区域后,平行斜面沿斜面向上的恒力大小变为F2,直至金属框到达斜面顶端(金属框上边与从AB重合)c试计算恒力 F1、F2所做总功的最小值? (F1、F2虽为恒力,但大小均未知) .
(1)30? 0.5m (2)0.50T (3)1.95J
解析试题分析:(1)在v2-s图中,分析s=1.6m之前的过程,由v2=2a1s
可知该过程线框的加速度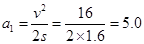 m/s2
m/s2
根据牛顿第二定律 mgsin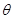 =ma1
=ma1
解得斜面倾角 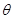 =30?
=30?
由于金属框只在s=1.6m~2.6m之间是匀速运动,可知金属框的运动情况是下边缘进入磁场时至上边缘刚好离开磁场时做匀速运动,所以匀强磁场的宽度 d=L=(2.6-1.6)/2=0.5m
(2)线框通过磁场时,设其速度为v1,由图可知,有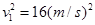 ,解得v1=4m/s
,解得v1=4m/s
在该过程中,有 BIL= mgsin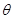 , 即
, 即  = mgsin
= mgsin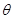
解得 B=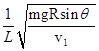 =0.50T
=0.50T
(3)金属框进入磁场前有 F1- mgsin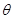 =ma4
=ma4
在磁场中运动有F1= mgsin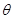 +F安
+F安
比较两式得F安= ma4
即 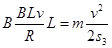 解得v=2m/s a4=2.5m/s2, 所以F安= ma4=0.25N,
解得v=2m/s a4=2.5m/s2, 所以F安= ma4=0.25N,
所以最小总功W总=F安×2d+mg(s1+s2+s3) sin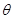 =1.95J
=1.95J
考点:导体切割磁感线时的感应电动势、安培力、匀变速直线运动的图象、牛顿第二定律

 名校联盟快乐课堂系列答案
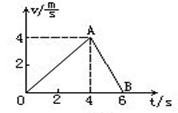
名校联盟快乐课堂系列答案甲乙两辆汽车在平直的公路上沿同一方向作直线运动,t=0时刻同时经过公路旁的同一个路标。在描述两车运动的v-t图中(如图),直线a、b分别描述了甲乙两车在0-20 s的运动情况。关于两车之间的位置关系,下列说法正确的是
| A.在0-10 s内两车逐渐靠近 |
| B.在10-20 s内两车逐渐远离 |
| C.在5-15 s内两车的位移相等 |
| D.在t=10 s时两车在公路上相遇 |
在如图所示的位移—时间图象和速度—时间图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点开始运动的情况,则下列说法正确的是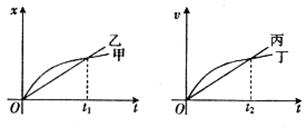
| A.甲车做曲线运动,乙车做直线运动 |
B.0~ 时间内,甲车通过的路程大于乙车通过的路程 时间内,甲车通过的路程大于乙车通过的路程 |
C.丙、丁两车在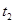 时刻相距最远 时刻相距最远 |
D.0~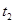 时间内,丙、丁两车的平均速度相等 时间内,丙、丁两车的平均速度相等 |
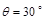 ,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值R=1.5Ω的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量m=0.4kg,电阻r=0.5Ω,重物的质量M=0.6kg。现将金属棒由静止释放,金属棒沿导轨上滑的距离与时间的关系图象如图乙所示。不计导轨电阻,g取10m/s2。求:
,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值R=1.5Ω的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量m=0.4kg,电阻r=0.5Ω,重物的质量M=0.6kg。现将金属棒由静止释放,金属棒沿导轨上滑的距离与时间的关系图象如图乙所示。不计导轨电阻,g取10m/s2。求: 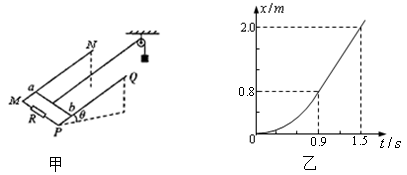
 —t图像如图乙,试求:(g=10m/s2)
—t图像如图乙,试求:(g=10m/s2)