题目内容
11.假设地球和金星都绕太阳做匀速圆周运动,已知金星到太阳的距离小于地球到太阳的距离,那么( )| A. | 地球公转的线速度大于金星公转的线速度 | |
| B. | 地球公转的角速度大于金星公转的角速度 | |
| C. | 地球公转的周期大于金星公转的周期 | |
| D. | 地球公转的加速度小于金星公转的加速度 |
分析 万有引力提供向心力,应用万有引力公式求出周期、线速度、加速度与角速度,然后分析答题.
解答 解:A、由牛顿第二定律得:$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$,解得$v=\sqrt{\frac{GM}{r}}$,由于${r}_{地}^{\;}>{r}_{金}^{\;}$,则${v}_{地}^{\;}<{v}_{金}^{\;}$,故A错误;
B、由牛顿第二定律得:$G\frac{Mm}{{r}_{\;}^{2}}=m{ω}_{\;}^{2}r$,解得$ω=\sqrt{\frac{GM}{{r}_{\;}^{3}}}$,由于${r}_{地}^{\;}>{r}_{金}^{\;}$,则${ω}_{地}^{\;}<{ω}_{金}^{\;}$,故B错误;
C、由牛顿第二定律得:$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,解得:$T=\sqrt{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{GM}}$,由于${r}_{地}^{\;}>{r}_{金}^{\;}$,则${T}_{地}^{\;}>{T}_{金}^{\;}$,故C正确;
D、由牛顿第二定律得:$G\frac{Mm}{{r}_{\;}^{2}}=ma$,解得:$a=\frac{GM}{{r}_{\;}^{2}}$,由于${r}_{地}^{\;}>{r}_{金}^{\;}$,则${a}_{地}^{\;}<{a}_{金}^{\;}$,故D正确;
故选:CD
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力是解题的前提,应用万有引力公式与牛顿第二定律可以解题,本题是一道常规题.

 阅读快车系列答案
阅读快车系列答案电源E(电动势为6V,内阻约为1Ω)
定值电阻R0(阻值约为5Ω)
电流表A(量程30mA,内阻约为0.5Ω)
电流表B(量程0.6A,内阻约为1Ω)
电压表C(量程8V,内阻约为5kΩ)
电压表D(量程4V,内阻约为3kΩ)
滑动变阻器F(阻值0-10Ω)
滑动变阻器G(阻值0-500Ω)
根据题中所给信息,请回答以下问题
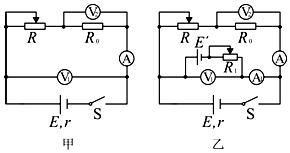
(1)电流表应选B,滑动变阻器应选F;(选填器材代号)
(2)该同学操作正确无误,用U1、U2、I分别表示电表
 、
、 、
、 的读数,其数据如表所示:
的读数,其数据如表所示:| I(A) | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 |
| U1(V) | 5.68 | 5.61 | 5.57 | 5.51 | 5.48 | 5.40 |
| U2(V) | 1.44 | 1.69 | 1.91 | 2.16 | 2.39 | 2.62 |
(3)该同学进一步利用一个辅助电源E′,采用如图乙所示的电路测量电源的电动势,测量过程中,调节R后再调节R1,使得A1的示数变为0,测得多组数据,这样,电源电动势值=电源电动势的真实值(填>、<或=).
| A. | 红光的频率大于紫光的频率 | |
| B. | 红光的频率小于紫光的频率 | |
| C. | 红光的波长小于紫光的波长 | |
| D. | 用同一装置做双缝干涉实验,红光的干涉条纹间距小于紫光的干涉条纹间距 |

| A. | 甲图是著名的泊松亮斑图案,这是光波的衍射现象 | |
| B. | 乙图中的彩虹是不同色光在水滴中折射率不同造成的 | |
| C. | 丙图的照相机镜头上涂有一层增透膜,增透膜利用了光的偏振原理 | |
| D. | 丁图是医学上的内窥镜,其核心部件光导纤维能传输光像信号,是利用光的全反射 |
 体育器材室里,篮球摆放在如图所示的由细杆组成的水平球架上,已知球架的宽度为d,每只篮球的质量为m,直径为D(D>d),不计球与球架之间的摩擦,则每只篮球对球架一侧的压力大小为( )
体育器材室里,篮球摆放在如图所示的由细杆组成的水平球架上,已知球架的宽度为d,每只篮球的质量为m,直径为D(D>d),不计球与球架之间的摩擦,则每只篮球对球架一侧的压力大小为( )| A. | $\frac{2mgd}{D}$ | B. | $\frac{mgD}{2d}$ | C. | $\frac{2mg\sqrt{{D}^{2}-{d}^{2}}}{D}$ | D. | $\frac{mgD}{2\sqrt{{D}^{2}-{d}^{2}}}$ |
 2016年8月16溶凌晨1时40分,全球首颗量子卫星-墨子号,在酒泉卫星发射中心成功发射,凭借此次发射,中国将在防黑客通讯技术方面远远领先于其全球竞争对手,如图所示,卫星最后定轨在离地面500km的预定圆周轨道,已知地球半径约6400km,同步卫星距地面约36000km,下列说法正确的是( )
2016年8月16溶凌晨1时40分,全球首颗量子卫星-墨子号,在酒泉卫星发射中心成功发射,凭借此次发射,中国将在防黑客通讯技术方面远远领先于其全球竞争对手,如图所示,卫星最后定轨在离地面500km的预定圆周轨道,已知地球半径约6400km,同步卫星距地面约36000km,下列说法正确的是( )| A. | 墨子号卫星的发射速度有可能为7.8km/s | |
| B. | 在相等时间内,墨子号卫星通过的弧长约为同步卫星通过弧长的8.5倍 | |
| C. | 墨子号卫星的向心加速度约为同步卫星的向心加速度的37.8倍 | |
| D. | 同步卫星绕地球转动周期,大于墨子号卫星绕地球转动周期 |
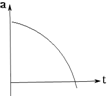
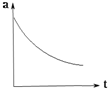
 球体在液体中下落时,液体对球的粘滞阻力与球的半径、速度及液体的种类有关,有F=6πηrv,其中物理量η为液体的粘滞系数,它还与液体的种类及温度有关,如图所示,现将一颗小钢珠由静止释放到盛有蓖麻油的足够深量筒中,下列描绘小钢珠在下沉过程中加速度大小与时间关系的图象可能正确的是( )
球体在液体中下落时,液体对球的粘滞阻力与球的半径、速度及液体的种类有关,有F=6πηrv,其中物理量η为液体的粘滞系数,它还与液体的种类及温度有关,如图所示,现将一颗小钢珠由静止释放到盛有蓖麻油的足够深量筒中,下列描绘小钢珠在下沉过程中加速度大小与时间关系的图象可能正确的是( )