题目内容
19.一质量为3×104kg的飞机在总长为2240m的飞机跑道上加速滑行,其牵引力恒为7.2×104N,受到的平均阻力为1.2×104N,若允许飞机在达到起飞速度的瞬间因故而停止起飞,立即关闭发动机后能以大小为5m/s2的恒定加速度减速而停下,飞机恰好不滑出跑道,则飞机加速过程发动机的最大功率为$5.76×1{0}_{\;}^{6}$W,牵引力做的功为$1.152×1{0}_{\;}^{8}$J.分析 根据牛顿第二定律和运动学公式求出匀加速运动的最大速度和位移,再根据P=Fv求发动机的最大功率,由W=Fx求牵引力做功;
解答 解:根据牛顿第二定律,得匀加速运动的加速度为:
${a}_{1}^{\;}=\frac{F-f}{m}=\frac{7.2×1{0}_{\;}^{4}-1.2×1{0}_{\;}^{4}}{3×1{0}_{\;}^{4}}m/{s}_{\;}^{2}$=$2m/{s}_{\;}^{2}$
设匀加速运动的位移为${x}_{1}^{\;}$,匀减速运动的位移为${x}_{2}^{\;}$,匀加速运动的末速度为v,根据位移关系有:
${x}_{1}^{\;}+{x}_{2}^{\;}=2240m$
根据速度位移关系,有:
${x}_{1}^{\;}=\frac{{v}_{\;}^{2}}{2{a}_{1}^{\;}}=\frac{{v}_{\;}^{2}}{4}$
${x}_{2}^{\;}=\frac{{v}_{\;}^{2}}{2{a}_{2}^{\;}}=\frac{{v}_{\;}^{2}}{10}$
$\frac{{v}_{\;}^{2}}{4}+\frac{{v}_{\;}^{2}}{10}=2240$
解得:v=80m/s
飞机加速过程中,发动机的最大功率为:
P=Fv=$7.2×1{0}_{\;}^{4}×80$=$5.76×1{0}_{\;}^{6}W$
匀加速运动的位移为:
${x}_{1}^{\;}=\frac{{v}_{\;}^{2}}{4}=\frac{8{0}_{\;}^{2}}{4}m=1600m$
牵引力做的功为:
$W=F•{x}_{1}^{\;}=7.2×1{0}_{\;}^{4}×1600$=$1.152×1{0}_{\;}^{8}J$
故答案为:$5.76×1{0}_{\;}^{6}$,$1.152×1{0}_{\;}^{8}$
点评 解决本题的关键是求解匀加速运动的末速度和位移,考查了牛顿第二定律和运动学公式、功和功率等知识点,要注意知识的综合运用.

 名校课堂系列答案
名校课堂系列答案
| A. | 6T0 | B. | 30T0 | C. | 60T0 | D. | 140T0 |
| A. | 用弹簧秤验证力的平行四边形定则 | |
| B. | 用伏安法测干电池电动势和内阻 | |
| C. | 用自由落体运动研究动能和重力势能转化的规律 | |
| D. | 用磁铁、线圈、灵敏电流计等探究感应电流产生的条件 |
| A. | 地球公转的线速度大于金星公转的线速度 | |
| B. | 地球公转的角速度大于金星公转的角速度 | |
| C. | 地球公转的周期大于金星公转的周期 | |
| D. | 地球公转的加速度小于金星公转的加速度 |
 “激流勇进”是一种常见的水上机动游乐设备,常见于主题游乐园中.游客们在一定安全装置的束缚下,沿着设计好的水道漂行.其间通常会有至少一次大幅度的机械提升和瞬时跌落.图中所示为游客们正坐在皮筏艇上从高处沿斜坡水道向下加速滑行,在此过程中下列说法正确的是( )
“激流勇进”是一种常见的水上机动游乐设备,常见于主题游乐园中.游客们在一定安全装置的束缚下,沿着设计好的水道漂行.其间通常会有至少一次大幅度的机械提升和瞬时跌落.图中所示为游客们正坐在皮筏艇上从高处沿斜坡水道向下加速滑行,在此过程中下列说法正确的是( )| A. | 合外力对游客做负功 | B. | 皮筏艇对游客不做功 | ||
| C. | 重力对游客做正功 | D. | 游客的机械能增加 |
| A. | 放射性元素的半衰期随温度升高而减小 | |
| B. | 光和电子都具有波粒二象性 | |
| C. | α粒子散射实验可以估算出原子核的数量级为10-10m | |
| D. | ${\;}_{90}^{234}Th$(钍)核衰变为${\;}_{91}^{234}Pa$(镤)核时,衰变前Th核质量等于衰变后Pa核与β粒子的总质量 |

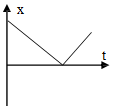

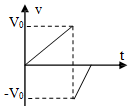
 光滑曲面末端与水平传送带相切,传送带两端相距L=2m,以v=1m/s的速度顺时针转动,一个可视为质点的质量m=1kg的物块A从曲面上高h=0.8m处由静止滑下,与静止在曲面末端可视为质点的质量m=1kg的物块B碰撞后粘在一起,碰后物块AB立即滑上传送带,一个横截面为等腰直角三角形的斜劈CDE的顶点D与传送带上表面在同一水平面,C点在传送带右端点的正下方,CE=DE=2.4m.物块与传送带间的动摩擦因数μ=0.2,g=10m/s2.求:
光滑曲面末端与水平传送带相切,传送带两端相距L=2m,以v=1m/s的速度顺时针转动,一个可视为质点的质量m=1kg的物块A从曲面上高h=0.8m处由静止滑下,与静止在曲面末端可视为质点的质量m=1kg的物块B碰撞后粘在一起,碰后物块AB立即滑上传送带,一个横截面为等腰直角三角形的斜劈CDE的顶点D与传送带上表面在同一水平面,C点在传送带右端点的正下方,CE=DE=2.4m.物块与传送带间的动摩擦因数μ=0.2,g=10m/s2.求: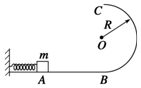 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相切,半圆形导轨的半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右的速度后脱离弹簧,当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍,之后向上运动恰能到达最高点C,C、O、B三点在同一竖直线上.(不计空气阻力)试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相切,半圆形导轨的半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右的速度后脱离弹簧,当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍,之后向上运动恰能到达最高点C,C、O、B三点在同一竖直线上.(不计空气阻力)试求: