题目内容
【题目】如图为一装放射源氡(![]() )的盒子,静止的氡核经过一次α衰变成钋(
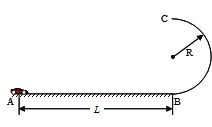
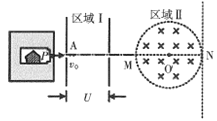
)的盒子,静止的氡核经过一次α衰变成钋(![]() ),产生的α粒子速率v0=1.0×107m/s,α粒子从小孔P射出后,经过A孔进入电场加速区域I,加速电压U=8×106V。从区域I射出的α粒子随后又从M点进入半径为r=
),产生的α粒子速率v0=1.0×107m/s,α粒子从小孔P射出后,经过A孔进入电场加速区域I,加速电压U=8×106V。从区域I射出的α粒子随后又从M点进入半径为r=![]() m的圆形匀强磁场区域II,MN为圆形匀强磁场的一条直径,该区域磁感应强度为B=0.2T,方向垂直纸面向里。圆形磁场右边有一竖直荧光屏与之相切于N点,粒子重力不计,比荷为
m的圆形匀强磁场区域II,MN为圆形匀强磁场的一条直径,该区域磁感应强度为B=0.2T,方向垂直纸面向里。圆形磁场右边有一竖直荧光屏与之相切于N点,粒子重力不计,比荷为![]() =5×107C/kg。
=5×107C/kg。
(1)请写出氡核衰变的核反应方程;
(2)求出α粒子经过圆形磁场后偏转的角度;
(3)求出α粒子打在荧光屏上的位置离N点的距离。
【答案】(1)![]() (2)60° (3)N点上方3m处
(2)60° (3)N点上方3m处
【解析】
(1)核反应过程核电荷数与质量数守恒,根据核电荷数与质量数守恒写核反应方程。
(2)α粒子在电场中加速,在磁场中做匀速圆周运动,应用动能定理与牛顿第二定律分析答题。
(3)根据几何知识求出α粒子打在荧光屏上的位置离N点的距离。
(1)由质量数与核电荷数守恒可知,反应方程式为:![]() ;
;
(2)α粒子在区域I电场中加速,由动能定理得:![]() ,其中v0=1.0×107m/s,
,其中v0=1.0×107m/s,
解得:![]()
α粒子离开电场区域后,以速度v,从M点沿MO方向进入磁场区域Ⅱ,在磁场中做匀速圆周运动
洛伦兹力提供向心力:![]()
联立方程并代入数据得:R=3m
α粒子的入射速度过圆心,由几何知识得:
![]() ,解得:
,解得:![]()
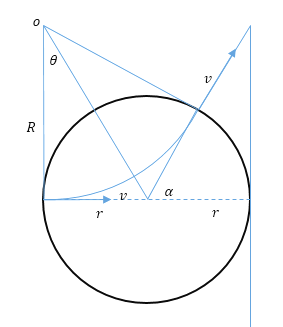
α粒子偏转角度为![]()
(3)由几何知识得:SNC=rtan60°=3m,
α粒子打在荧光屏上的N点上方3m处;

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目