题目内容
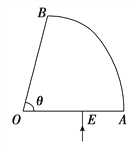
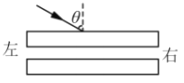
【题目】如图所示,固定在水平面上长度为L的木板与竖直放置的半径为R的半圆形光滑轨道BC相切于B点,在木板左端A处静止放置一个质量为m的小物块(可视为质点)。一个质量为![]() =0.2m的子弹以水平速度
=0.2m的子弹以水平速度![]() 射向物块,击中物块后恰好能与物块一起运动到C点,最终落在木板上的D点(图中未画出)。已知重力加速度为g。求:
射向物块,击中物块后恰好能与物块一起运动到C点,最终落在木板上的D点(图中未画出)。已知重力加速度为g。求:

(1)子弹击中物块后物块的速度和此过程中系统损失的机械能;
(2)物块通过半圆形轨道最低点B时对轨道的压力以及物块与木板间的动摩擦因数;
(3)D点与B点的距离及物块落在木板上前的瞬时速度与水平方向间夹角的正切值。
【答案】(1)![]() ;
;![]() (2)F=7.2mg,方向竖直向下;
(2)F=7.2mg,方向竖直向下;![]() (3)x=2R;2
(3)x=2R;2
【解析】(1)由动量守恒定律得![]() ,解得
,解得![]() ;
;
子弹击中物块过程中系统损失的机械能![]() ;
;
(2)由于物块恰好能够通过半圆形轨道的最高点C,所以有![]() ,
,
解得![]() ;
;
物块从B点到C点的过程中,由机械能守恒定律得![]() ;
;
设在B点轨道对物块的作用力为F,由牛顿第二定律有![]() ,
,
联立解得![]() ,方向竖直向下;
,方向竖直向下;
由牛顿第三定律可知物块通过半圆形轨道最低点B时对轨道的压力为7.2mg,方向竖直向下;
对物块在木板上的运动,由动能定理得![]() ,解得
,解得![]() ;
;
(3)设物块落在木板上的位置与B点的距离为x,由平抛运动的规律得![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,解得
,解得![]()

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目