题目内容
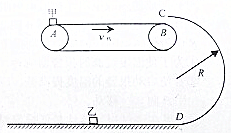
11. 在某电视台娱乐节目中,要求选手从较高的平台上以水平速度v0跃出,落在水平传送带上,如图所示.已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,人落到传送带上后立即就与传送带相对静止.选手经过△t=0.5s反应时间,立刻以方向向右的加速度a=2m/s2跑至传送带最右端B.
在某电视台娱乐节目中,要求选手从较高的平台上以水平速度v0跃出,落在水平传送带上,如图所示.已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,人落到传送带上后立即就与传送带相对静止.选手经过△t=0.5s反应时间,立刻以方向向右的加速度a=2m/s2跑至传送带最右端B.(1)要使选手落在传送带上,求v0的最小值.
(2)若传送带静止,选手以v0=3m/s水平速度从平台跃出,求选手从开始跃出到跑至B端所需时间.
(3)若传送带以u=1m/s的恒定速度向左运动,选手若要能到达传送带右端,则从高台上跃出的水平速度v1至少多大?
分析 (1)从开始跃出到跑至传送带右端经历的时间经历两个过程:平抛运动和匀加速直线运动.平抛运动的时间可以通过竖直方向去求,因为平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动,结合水平位移求出选手的初速度;
(2)在水平方向上做匀速直线运动,求出水平位移,然后再求出匀加速运动的位移以及时间;
(3)选手平抛运动到传送带上后,在反应时间内跟传送带一起向左做匀速,然后以2m/s2的加速度向左做匀减速直线运动到0,如果在这段时间内未掉入水中,则不会落入水中,以后向右做初速度为0的匀加速直线运动.
解答 解:(1)选手离开平台后做平抛运动
在竖直方向上有:H=$\frac{1}{2}$gt12,得t1=$\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×1.8}{10}}$=0.6 s
最小值:${v}_{0}=\frac{{s}_{0}}{{t}_{1}}=\frac{1.2}{0.6}=2$m/s
(2)选手离开平台后做平抛运动
在水平方向上有:s1=v0t1=1.8 m
在传送带上做匀加速运动的位移满足:L0-(s1-s0)=$\frac{1}{2}$at22,得t2=4.5 s
则选手运动的总时间t=t1+t2+△t=5.6 s
(3)落到传送带上0.5 s反应时间内向左发生的位移为:s2=u△t=0.5 m
然后向左减速至速度为零,又向左发生位移s3=$\frac{{u}^{2}}{2a}$=0.25 m
不从传送带上掉下须满足:s≥s0+s2+s3=1.95 m
则v1≥$\frac{s}{{t}_{1}}$=3.25 m/s
答:(1)要使选手落在传送带上,v0的最小值是2m/s.
(2)若传送带静止,选手以v0=3m/s水平速度从平台跃出,选手从开始跃出到跑至B端所需时间是5.6s.
(3)若传送带以u=1m/s的恒定速度向左运动,选手若要能到达传送带右端,则从高台上跃出的水平速度v1至少是3.25m/s.
点评 该题将传送带问题与平抛运动相结合,解决本题的关键分析出选手的运动情况,特别是初速度向左运动时,选手不落水的临界条件要找对,然后根据平抛运动和运动学公式求解.

 阅读快车系列答案
阅读快车系列答案| A. | 同时的绝对性与同时的相对性 | |
| B. | 运动的时钟变慢与运动的尺子缩短 | |
| C. | 时间间隔的绝对性与空间距离的绝对性 | |
| D. | 狭义相对性原理与光速不变原理 |
| A. | 做曲线运动的物体,其受力的方向一定发生变化 | |
| B. | 做曲线运动的物体,其受力的大小一定发生变化 | |
| C. | 第2s末和第3s初是指同一时刻 | |
| D. | 第2s内与前2s内是指同一秒时间 |
| A. | 质量可以不同 | B. | 离地高度不同 | C. | 轨道平面不同 | D. | 运行速率不同 |
| A. | 体积很小的带电体就是点电荷 | |
| B. | 元电荷就是指一个电子或一个质子 | |
| C. | 凡计算真空中两个静止点电荷间的相互作用,都可以使用公式F=k$\frac{{{q_1}{q_2}}}{r^2}$ | |
| D. | 相互作用的两个点电荷,不论电荷量是否相等,它们之间的库仑力大小一定相等 |
| A. | 物体在水平面上做匀速直线运动,合力对物体做的功 | |
| B. | 重力对自由落体运动的物体做的功 | |
| C. | 物体在水平面上运动,水平面对物体的支持力所做的功 | |
| D. | 物体在固定斜面上沿斜面下滑时,斜面对物体的支持力做的功 |
 如图所示,质量为m的小物块甲轻放在以v传=5m/s向右匀速运动的传送带的左端A位置,当物块运动到传送带右端B位置后从C点沿圆弧切线进入半径R=0.2m的竖直光滑半圆形轨道,到达轨道最低点D后滑上水平光滑轨道,并与静止在水平面上质量为km的小物块乙发生弹性碰撞.现测得物块甲刚滑到轨道最低点D时对水平轨道的压力N=13.5mg.物块甲与传动带间的动摩擦因数μ=0.4(g取10m/s2),求:
如图所示,质量为m的小物块甲轻放在以v传=5m/s向右匀速运动的传送带的左端A位置,当物块运动到传送带右端B位置后从C点沿圆弧切线进入半径R=0.2m的竖直光滑半圆形轨道,到达轨道最低点D后滑上水平光滑轨道,并与静止在水平面上质量为km的小物块乙发生弹性碰撞.现测得物块甲刚滑到轨道最低点D时对水平轨道的压力N=13.5mg.物块甲与传动带间的动摩擦因数μ=0.4(g取10m/s2),求: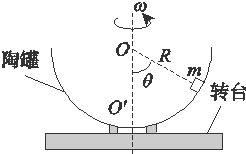 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.