题目内容
20. 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.(1)若ω=ω0,小物块受到的摩擦力恰好为零,求ω0;
(2)若ω=(1±k)ω0,且0<k≤1,求小物块受到的摩擦力大小和方向.
分析 (1)若ω=ω0,小物块受到的摩擦力恰好为零,靠重力和支持力的合力提供向心力,根据牛顿第二定律求出角速度的大小.
(2)当ω>ω0,重力和支持力的合力不够提供向心力,摩擦力方向沿罐壁切线向下,根据牛顿第二定律求出摩擦力的大小.当ω<ω0,重力和支持力的合力大于向心力,则摩擦力的方向沿罐壁切线向上,根据牛顿第二定律求出摩擦力的大小.
解答 解:(1)小物块在水平面内做匀速圆周运动,当小物块受到的摩擦力恰好等于零时,小物块所受的重力和陶罐的支持力的合力提供圆周运动的向心力,有
mgtanθ=mω${\;}_{0}^{2}$•Rsinθ
解得ω0=$\sqrt{\frac{2g}{R}}$
(2)当ω=(1+k)ω0时,小物块受到的摩擦力沿陶罐壁切线向下,设摩擦力的大小为f,陶罐壁对小物块的支持力为FN,沿水平和竖直方向建立坐标系,则:
水平方向:FNsinθ+fcosθ=mω2•Rsinθ
竖直方向:FNcosθ-fsinθ-mg=0
代入数据解得:f=$\frac{\sqrt{3}k(2+k)}{2}$mg
同理,当ω=(1-k)ω0时,小物块受到的摩擦力沿陶罐壁切线向上,则:
水平方向:FNsinθ-fcosθ=mω2•Rsinθ
竖直方向:FNcosθ+fsinθ-mg=0
代入数据解得:f=$\frac{\sqrt{3}k(2-k)}{2}$mg.
答:
(1)ω0为$\sqrt{\frac{2g}{R}}$.
(2)当ω=(1+k)ω0时,摩擦力方向沿罐壁切线向下,大小为$\frac{\sqrt{3}k(2+k)}{2}$mg.当ω=(1-k)ω0时,摩擦力方向沿罐壁切线向上,大小为$\frac{\sqrt{3}k(2-k)}{2}$mg.
点评 解决本题的关键搞清物块做圆周运动向心力的来源,结合牛顿第二定律,抓住竖直方向上合力为零,水平方向上的合力提供向心力进行求解.

| A. | 三个力的合力的可能为17N | B. | 三个力的合力的最小值为1N | ||
| C. | 三个力的合力不可能为9N | D. | 三个力的合力不可能为3N |
| A. | 该船渡河所用时间至少是10s | |
| B. | 该船渡河最小速率是4m/s | |
| C. | 河水的流速越大,渡河的时间越长 | |
| D. | 该船不可能沿垂直于河岸的航线抵达对岸 |
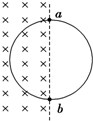 用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的一条直径.如图所示,在ab的左侧存在一个均匀变化的匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0).则( )
用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的一条直径.如图所示,在ab的左侧存在一个均匀变化的匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0).则( )| A. | 圆环中产生逆时针方向的感应电流 | |
| B. | 圆环具有扩张的趋势 | |
| C. | 圆环中感应电流的大小为$\frac{krs}{4ρ}$ | |
| D. | 图中a、b两点间的电势差Uab=|$\frac{1}{4}$kπr2| |
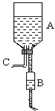 图为医院为病人输液的部分装置,图中A为输液瓶,B为滴壶,C为进气管,与大气相通.则在输液过程中(瓶A中尚有液体),下列说法正确的是( )
图为医院为病人输液的部分装置,图中A为输液瓶,B为滴壶,C为进气管,与大气相通.则在输液过程中(瓶A中尚有液体),下列说法正确的是( )| A. | 瓶A中上方气体的压强随液面的下降而减小 | |
| B. | 瓶A中液面下降,A中上方气体的压强变大 | |
| C. | 滴壶B中的气体压强随A中液面的下降而减小 | |
| D. | 在瓶中药液输完以前,滴壶B中的气体压强保持不变 |
 在某电视台娱乐节目中,要求选手从较高的平台上以水平速度v0跃出,落在水平传送带上,如图所示.已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,人落到传送带上后立即就与传送带相对静止.选手经过△t=0.5s反应时间,立刻以方向向右的加速度a=2m/s2跑至传送带最右端B.
在某电视台娱乐节目中,要求选手从较高的平台上以水平速度v0跃出,落在水平传送带上,如图所示.已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,人落到传送带上后立即就与传送带相对静止.选手经过△t=0.5s反应时间,立刻以方向向右的加速度a=2m/s2跑至传送带最右端B.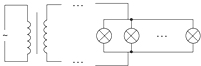 一台交流发电机产生u=220$\sqrt{2}$•sin 100πt V的交流电压,其内阻不计,经过变压器变压后通过总电阻r=2Ω的长导线给彩灯供电,如图所示.60只彩色小灯泡并联在电路中,每只灯泡都是“6V,0.25W”,灯泡均正常发光.(其余电阻不计)试求:
一台交流发电机产生u=220$\sqrt{2}$•sin 100πt V的交流电压,其内阻不计,经过变压器变压后通过总电阻r=2Ω的长导线给彩灯供电,如图所示.60只彩色小灯泡并联在电路中,每只灯泡都是“6V,0.25W”,灯泡均正常发光.(其余电阻不计)试求: