题目内容
(2006?福建模拟)微观粒子之间的相互作用都是通过交换某种粒子(如光子、中间玻色子、胶子)来实现的.粒子间的排斥作用可以简化为如下的一个力学模型来描述:
水平冰面上两个质量均为m的滑冰者A和B,分别以大小为υA和υB的水平速度相向运动(如图甲).当它们趋近到一定距离时,为避免相撞,A立即沿水平方向向B扔出一个动量大小为p(相对地面,下同)、质量可以忽略的小球,小球在B手中停留一段时间T后又以大小相同的动量p水平扔回A手中,A又经相同时间T再次以同样大小的动量水平扔给B,并不断重复上述过程,直至两个滑冰者避免了相撞.设水平冰面摩擦不计,除小球在A、B手中停留的时间T外,不计空中飞行的时间,以水平向右为正方向.求:
(1)滑冰者B第一次把球接到手中时A、B的速度;
(2)从A开始扔球算起,球在A、B之间至少被扔出几次才可以避免两个滑冰者相撞?
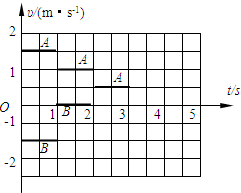
(3)设m=60kg,υA=2m/s,υB=1m/s,p=30kg?m/s,T=1s,t=0时A刚好扔出小球,试在图乙给出的同一个υ-t坐标图上,画出问(2)过程中A、B两个滑冰者的速度随时间变化的υ-t图线(不要求写出计算过程,只按画出的图线评分,但图线上必须注明A和B)

水平冰面上两个质量均为m的滑冰者A和B,分别以大小为υA和υB的水平速度相向运动(如图甲).当它们趋近到一定距离时,为避免相撞,A立即沿水平方向向B扔出一个动量大小为p(相对地面,下同)、质量可以忽略的小球,小球在B手中停留一段时间T后又以大小相同的动量p水平扔回A手中,A又经相同时间T再次以同样大小的动量水平扔给B,并不断重复上述过程,直至两个滑冰者避免了相撞.设水平冰面摩擦不计,除小球在A、B手中停留的时间T外,不计空中飞行的时间,以水平向右为正方向.求:
(1)滑冰者B第一次把球接到手中时A、B的速度;
(2)从A开始扔球算起,球在A、B之间至少被扔出几次才可以避免两个滑冰者相撞?
(3)设m=60kg,υA=2m/s,υB=1m/s,p=30kg?m/s,T=1s,t=0时A刚好扔出小球,试在图乙给出的同一个υ-t坐标图上,画出问(2)过程中A、B两个滑冰者的速度随时间变化的υ-t图线(不要求写出计算过程,只按画出的图线评分,但图线上必须注明A和B)

分析:(1)第一次A扔球,A与球的动量守恒,B接球过程,B与球的动量守恒,根据动量守恒定律列式求解;
(2)同理可得,第二次B扔球、A接球后两球的速度,总结规律得到n次扔球、接球后两球的速度υAn和υBn.要使A、B不相撞且扔球次数最少,应满足υAn=υBn,即可得到满足A、B不相撞所需的最少扔球的次数.
(3)分段作两个滑冰者的速度随时间变化的υ-t图线.
(2)同理可得,第二次B扔球、A接球后两球的速度,总结规律得到n次扔球、接球后两球的速度υAn和υBn.要使A、B不相撞且扔球次数最少,应满足υAn=υBn,即可得到满足A、B不相撞所需的最少扔球的次数.
(3)分段作两个滑冰者的速度随时间变化的υ-t图线.
解答:解:(1)取水平向右为正方向,第一次A扔球、B接球,设A扔球后速度为,B接球后速度为,由动量守恒定律有
:A扔球过程,有:mυA=mυA1+p
解得:υA1=υA-
B接球过程,有:-mυB+p=mυB1
解得:υB1=-υB+
(2)第二次B扔球、A接球,设B扔球后速度为υB2,A接球后速度为υA2,则由动量守恒定律:
mυB1=mυB2-p
解得:υB2=υB1+
=-υB+
mυA1-p=mυA2
解得:υA2=υA1-
=υA-
设n次扔球、接球后.A的速度为υAn,B的速度为υBn,则由上述推理可得:
υAn=υA-
υBn=-υB+
要使A、B不相撞且扔球次数最少,应满足:υAn=υBn
因此,满足A、B不相撞所需的最少扔球次数为:n=
讨论:
①当
为整数时,n取
;
②当
不为整数时,取
+1
(3)如图所示
答:(1)滑冰者B第一次把球接到手中时A、B的速度分别为υA-
和-υB+
;
(2)从A开始扔球算起,球在A、B之间至少被扔出
或
+1次才可以避免两个滑冰者相撞.
(3)A、B两个滑冰者的速度随时间变化的υ-t图线如图所示.
:A扔球过程,有:mυA=mυA1+p
解得:υA1=υA-
| p |
| m |
B接球过程,有:-mυB+p=mυB1
解得:υB1=-υB+
| p |
| m |
(2)第二次B扔球、A接球,设B扔球后速度为υB2,A接球后速度为υA2,则由动量守恒定律:
mυB1=mυB2-p
解得:υB2=υB1+
| p |
| m |
| 2p |
| m |
mυA1-p=mυA2
解得:υA2=υA1-
| p |
| m |
| 2p |
| m |
设n次扔球、接球后.A的速度为υAn,B的速度为υBn,则由上述推理可得:
υAn=υA-
| np |
| m |
υBn=-υB+
| nP |
| m |
要使A、B不相撞且扔球次数最少,应满足:υAn=υBn
因此,满足A、B不相撞所需的最少扔球次数为:n=
| m(vA+vB) |
| 2p |
讨论:
①当
| m(vA+vB) |
| 2p |
| m(vA+vB) |
| 2p |
②当
| m(vA+vB) |
| 2p |
| m(vA+vB) |
| 2p |
(3)如图所示

答:(1)滑冰者B第一次把球接到手中时A、B的速度分别为υA-
| p |
| m |
| p |
| m |
(2)从A开始扔球算起,球在A、B之间至少被扔出
| m(vA+vB) |
| 2p |
| m(vA+vB) |
| 2p |
(3)A、B两个滑冰者的速度随时间变化的υ-t图线如图所示.
点评:解决本题的关键掌握动量守恒定律的条件,合理选择研究的过程,采用归纳法运用动量守恒定律进行求解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
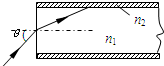 (2006?福建模拟)2008年奥运会,光纤通信网将覆盖所有的奥运场馆,为各项比赛提供安全、可靠的通信服务.光纤通信采用的光导纤维是由内芯和外套组成,其中内芯的折射率为n1,外套的折射率为n2,下面说法正确的是( )
(2006?福建模拟)2008年奥运会,光纤通信网将覆盖所有的奥运场馆,为各项比赛提供安全、可靠的通信服务.光纤通信采用的光导纤维是由内芯和外套组成,其中内芯的折射率为n1,外套的折射率为n2,下面说法正确的是( )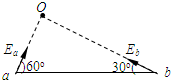 (2006?福建模拟)如图,真空中O点有一点电荷,它产生的电场中有a、b两点,a点的场强大小为Ea,方向与ab连线成60°角,b点的场强大小为Eb,方向与连线成30°角.则关于a、b两点的场强大小及电势φa、φb的高低关系正确的是( )
(2006?福建模拟)如图,真空中O点有一点电荷,它产生的电场中有a、b两点,a点的场强大小为Ea,方向与ab连线成60°角,b点的场强大小为Eb,方向与连线成30°角.则关于a、b两点的场强大小及电势φa、φb的高低关系正确的是( )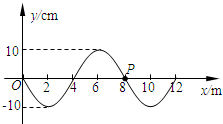 (2006?福建模拟)如图所示是一列简谐横波在t=0时刻的图象,经过0.4s时间恰好再次出现图示的波形.以下可确定的是( )
(2006?福建模拟)如图所示是一列简谐横波在t=0时刻的图象,经过0.4s时间恰好再次出现图示的波形.以下可确定的是( )