题目内容
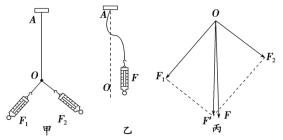
【题目】如图所示，长为3l的不可伸长的轻绳，穿过一长为l的竖直轻质细管，两端分别拴着质量为m、2m的小球A和小物块B，开始时B静止在细管正下方的水平地面上。保持细管竖直用手轻轻摇动细管，稳定后A在水平面内做匀速圆周运动而B保持静止状态。某时刻B静止在地面上且对地面的压力恰好为零。已知重力加速度为g，不计一切阻力。求：
该时刻连接A的轻绳与竖直方向的夹角
；
该时刻A的线速度大小v；
从该时刻起轻摇细管使B升高到离地高度为
处保持静止，求B上升过程中手对A、B系统做的功。
【答案】
；
；
。
【解析】
(1)对B根据平衡求绳子的拉力；对A球分析，由力的平衡条件可求绳与竖直方向夹角θ；
(2)对A水平方向做圆周运动，利用牛顿第二定律列式求解；
(3)由力的平衡条件和牛顿第二定律并结合功能关系列式联立可求整个过程中人对A、B系统做的功。
（1）B对地面刚好无压力，故此时绳子的拉力为
对A受力分析如图所示：
在竖直方向合力为零，故
代入数据解得：
（2）A球水平方向做圆周运动，由牛顿第二定律得：
代入数据解得：
（3）当B上升
时，拉A的绳长为
，此时对水平方向上有：
联立解得：
由几何关系可得A相对于原来的高度下降的距离：
B物体重力势能的增加量：
A物体重力势能的减少量：
A物体动能的增加量
对系统运用功能关系可得手对系统做的功：
练习册系列答案
相关题目
