题目内容
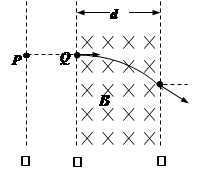
如右图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域,分别存在着等大反向的匀强磁场,磁感应强度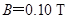 ,磁场区域半径
,磁场区域半径 ,左侧区圆心为
,左侧区圆心为 ,磁场向里,右侧区圆心为
,磁场向里,右侧区圆心为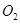 ,磁场向外.两区域切点为C.今有质量
,磁场向外.两区域切点为C.今有质量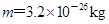 .带电荷量
.带电荷量 的某种离子,从左侧区边缘的A点以速度
的某种离子,从左侧区边缘的A点以速度 正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求: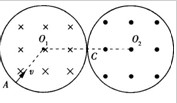
(1)该离子通过两磁场区域所用的时间.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为多大?(侧移距离指垂直初速度方向上移动的距离)
(1) 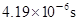 (2)2 m
(2)2 m
解析试题分析:(1)离子在磁场中做匀速圆周运动,在左右两区域的运动轨迹是对称的,如右图,设轨迹半径为R,圆周运动的周期为T.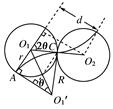
由牛顿第二定律 ①
①
又 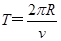 ②
②
联立①②得: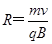 ③
③ ④
④
将已知代入③得 ⑤
⑤
由轨迹图知: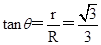 ,则
,则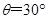
则全段轨迹运动时间: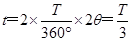
联立④⑥并代入已知得: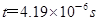
(2)在图中过O2向AO1作垂线,联立轨迹对称关系侧移总距离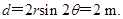
考点:带电粒子在匀强磁场中的运动;
点评:本题是有界磁场问题,关键是画出粒子的运动轨迹,运用几何知识求解半径.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
一个小球做自由落体运动,在第1s内重力做功为W1,在第2s内重力做功为W2;在第1s末重力的瞬时功率为P1,在第2s末重力的瞬时功率做功为P2,则W1:W2及P1:P2分别等于( )
| A.1:1,1:1 | B.1:2,1:3 | C.1:3;1:2 | D.1:4,1:2 |
下列关于力做功的说法中正确的是( )
| A.人用力F=300N将足球踢出,球在空中飞行40m,人对足球做功1200J |
| B.人用力推物体,但物体未被推动,人对物体做功为零 |
| C.物体竖直上升时,重力不做功 |
| D.只有恒力才能做功,变力不能做功 |
有一半径r =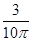 m的圆柱体绕竖直轴OO´以角速度ω=8
m的圆柱体绕竖直轴OO´以角速度ω=8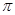 rad/s匀速转动,今用水平力F把质量m=l.2kg的物体A压在圆柱体的侧面,由于受挡板上竖直光滑槽的作用,物体A在水平方向上不能随圆柱体转动,而以v0=1.8m/s的速率匀速下滑,如图所示。已知物体A与圆柱体间的动摩擦因数μ=0.25,g取l0m/s2。下列说法中正确的有
rad/s匀速转动,今用水平力F把质量m=l.2kg的物体A压在圆柱体的侧面,由于受挡板上竖直光滑槽的作用,物体A在水平方向上不能随圆柱体转动,而以v0=1.8m/s的速率匀速下滑,如图所示。已知物体A与圆柱体间的动摩擦因数μ=0.25,g取l0m/s2。下列说法中正确的有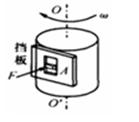
| A.圆柱体对A的摩擦力大小为20N |
| B.水平力F大小为48N |
| C.圆柱体转动一周过程中克服摩擦力做功为9.6J |
| D.圆柱体转动一周过程中,物体A克服摩擦力做功为5.4J |