题目内容
14.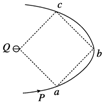 负点电荷Q固定在正方形的一个顶点上,带电粒子P仅在该电荷的电场力作用下运动时,恰好能经过正方形的另外三个顶点a、b、c,如图所示,则( )
负点电荷Q固定在正方形的一个顶点上,带电粒子P仅在该电荷的电场力作用下运动时,恰好能经过正方形的另外三个顶点a、b、c,如图所示,则( )| A. | 粒子P带负电 | |
| B. | a、b、c三点的电势高低关系是φa=φc>φb | |
| C. | 粒子P由a到b电势能减少,由b到c电势能增加 | |
| D. | 粒子P在a、b、c三点的加速度大小之比是2:1:2 |
分析 电荷受到的合力指向轨迹的内侧,根据轨迹弯曲方向判断出粒子与点电荷是异种电荷,它们之间存在引力,根据点电荷的电场线的特点,Q与ac距离相等,都小于b,故B点的电势高于ac两点的电势.应用牛顿第二定律求出加速度之间的关系.
解答 解:A、根据轨迹弯曲方向判断出带电粒子与负电荷之间存在引力,它与负点电荷是异种电荷,故带正电荷,故A错误;
B、根据点电荷电场线的特点,Q与a、c间的距离相等,都小于b,故b点的电势高于a、c两点的电势,即有φa=φc<φb.故B错误;
C、正电荷P从a到b,电势升高,电势能就增加;反之,从b到c电势能减小,故C错误;
D、粒子P在a、b、c三点时的加速度大小要根据库仑定律求出库仑力.由图可知,ra=rc=$\frac{\sqrt{2}}{2}$rb,
代入库仑定律F=K$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$,可得:$\frac{{F}_{a}}{{F}_{b}}$=$\frac{{r}_{b}^{2}}{{r}_{a}^{2}}$,由牛顿第二定律:$\frac{{a}_{a}}{{a}_{b}}$=$\frac{2}{1}$.又aa=ac,则a、b、c三点的加速度大小之比是2:1:2,故D正确.
故选:D.
点评 本题属于电场中轨迹问题,考查分析推理能力.根据轨迹的弯曲方向,判断出电荷受到的电场力指向轨迹内侧.进而判断出电荷是正电荷.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )
如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )
 如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )
如图所示,小球从光滑圆弧曲面上的A处由静止下滑,恰好能通过半径为r的光滑圆形轨道的最高点C,已知重力加速度为g,则( )| A. | 小球经过最高点C的速度为$\sqrt{gr}$ | |
| B. | 小球经过最高点时受到的向心力为0 | |
| C. | A点相对于B点的高度h=$\frac{5}{2}$r | |
| D. | 小球经过圆心轨道的最低点B时的加速度可能小于g |
2.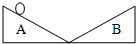 如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
 如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )| A. | 高度 | B. | 动能 | C. | 势能 | D. | 能量 |
9. 图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
 图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )| A. | A、B两点的角速度大小跟半径成反比 | |
| B. | A、B两点的角速度大小跟半径成正比 | |
| C. | A、C两点的线速度大小跟半径成反比 | |
| D. | A、C两点的线速度大小跟半径成正比 |
6.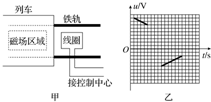 如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )
如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )
 如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )
如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )| A. | 匀速运动 | B. | 匀加速运动 | C. | 匀减速运动 | D. | 变加速运动 |
3.NBA篮球赛非常精彩,吸引了众多观众.2012-2013赛季总决赛第六场中,雷阿伦在终场前5.2s的时候,把球投出且准确命中,把比赛拖入加时从而让热火获得比赛的胜利.如果雷阿伦投篮过程中对篮球做功为W,出手高度为h1,篮筐距地面高度为h2,篮球的质量为m,空气阻力不计,则篮球进筐时的动能为( )
| A. | W+mgh1-mgh2 | B. | W+mgh2-mgh1 | C. | mgh1+mgh2-W | D. | mgh2-mgh1-W |
4. “电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
 “电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )
“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成.偏转器是由两个相互绝缘、半径分别为RA和RB的同心金属半球面A和B构成,A、B为电势值不等的等势面电势分别为φA和φB,其过球心的截面如图所示.一束电荷量为e、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射,进入偏转电场区域,最后到达偏转器右端的探测板N,其中动能为Ek0的电子沿等势面C做匀速圆周运动到达N板的正中间.忽略电场的边缘效应.下列说法中正确的是( )| A. | A球面电势比B球面电势低 | |
| B. | 电子在AB间偏转电场中做匀变速运动 | |
| C. | 等势面C所在处电场强度的大小为E=$\frac{{4{E_{k0}}}}{{e({{R_A}+{R_B}})}}$ | |
| D. | 等势面C所在处电势大小为$\frac{{{φ_A}+{φ_B}}}{2}$ |
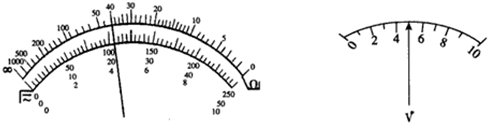
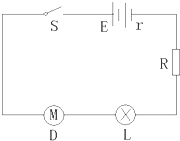 研究电动机的特性时,将电动机接成如图所示电路.电源电动势E=20V,内阻r=lΩ,当接入固定电阻R=4Ω时,电路中标有“3V,6W”的灯泡L和内阻RD=0.5Ω的小型直流电动机D都恰能正常工作.试求:
研究电动机的特性时,将电动机接成如图所示电路.电源电动势E=20V,内阻r=lΩ,当接入固定电阻R=4Ω时,电路中标有“3V,6W”的灯泡L和内阻RD=0.5Ω的小型直流电动机D都恰能正常工作.试求: