��Ŀ����
4�� ��������������������Ҫ�ɴ�������еĵ���ƫת����̽�����ɣ�ƫת�������������Ե���뾶�ֱ�ΪRA��RB��ͬ�Ľ���������A��B���ɣ�A��BΪ����ֵ���ȵĵ�������Ʒֱ�Ϊ��A�ͦ�B��������ĵĽ�����ͼ��ʾ��һ�������Ϊe������Ϊm�ĵ����Բ�ͬ�Ķ��ܴ�ƫת�����M�����м�С�״�ֱ���䣬����ƫת�糡�������ƫת���Ҷ˵�̽���N�����ж���ΪEk0�ĵ����ص�����C������Բ���˶�����N������м䣮���Ե糡�ı�ԵЧӦ������˵������ȷ���ǣ�������
��������������������Ҫ�ɴ�������еĵ���ƫת����̽�����ɣ�ƫת�������������Ե���뾶�ֱ�ΪRA��RB��ͬ�Ľ���������A��B���ɣ�A��BΪ����ֵ���ȵĵ�������Ʒֱ�Ϊ��A�ͦ�B��������ĵĽ�����ͼ��ʾ��һ�������Ϊe������Ϊm�ĵ����Բ�ͬ�Ķ��ܴ�ƫת�����M�����м�С�״�ֱ���䣬����ƫת�糡�������ƫת���Ҷ˵�̽���N�����ж���ΪEk0�ĵ����ص�����C������Բ���˶�����N������м䣮���Ե糡�ı�ԵЧӦ������˵������ȷ���ǣ�������| A�� | A������Ʊ�B������Ƶ� | |
| B�� | ������AB��ƫת�糡�����ȱ����˶� | |
| C�� | ������C���ڴ��糡ǿ�ȵĴ�СΪE=$\frac{{4{E_{k0}}}}{{e��{{R_A}+{R_B}}��}}$ | |
| D�� | ������C���ڴ����ƴ�СΪ$\frac{{{��_A}+{��_B}}}{2}$ |
���� ����������Բ���˶����糡���ṩ�����������������ķ�����糡�ķ����෴����ţ�ٵڶ����ɺ���������ʽ���
�õ糡�Ƿ���״�糡���ڲ�ĵ糡���ܣ��糡ǿ�ȴ��ϵ��Ʋ�ı���ʽ���ɵó�C��ĵ��ƴ�С��
��� �⣺A������������Բ���˶����糡���ṩ�������������ķ�����糡�ķ����෴������B��ĵ��ƽϸߣ���A��ȷ��
B������������Բ���˶����ܵ��ĵ糡��ʼ��ʼ��Բ�ģ��DZ��������Ե����ڵ糡�е��˶������ȱ����˶�����B����
C�������ڵ�����C���ڴ�������Բ���˶����糡���ṩ��������
$eE=\frac{m{v}^{2}}{R}$
�֣�$R=\frac{{R}_{A}+{R}_{B}}{2}$��
${E}_{K0}=\frac{1}{2}m{v}^{2}$
��������3ʽ���ã�$E=\frac{4{E}_{k0}}{e��{R}_{A}+{R}_{B}��}$����C��ȷ��
D���õ糡�Ƿ���״�糡���ڲ�ĵ糡���ܣ��糡ǿ�ȴ�����UBC��UCA��������C-��B����C-��A�����ԣ���C��$\frac{{{��_A}+{��_B}}}{2}$����D����
��ѡ��AC
���� ���⿼����������ڷ���״�糡�е��˶���糡������������Ĺؼ��ǵ糡���ṩ��������д����Ӧ�ı���ʽ��������ȷ���

��ϰ��ϵ�д�
 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�
�����Ŀ
14��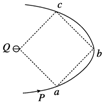 ������Q�̶��������ε�һ�������ϣ���������P���ڸõ�ɵĵ糡���������˶�ʱ��ǡ���ܾ��������ε�������������a��b��c����ͼ��ʾ��������
������Q�̶��������ε�һ�������ϣ���������P���ڸõ�ɵĵ糡���������˶�ʱ��ǡ���ܾ��������ε�������������a��b��c����ͼ��ʾ��������
 ������Q�̶��������ε�һ�������ϣ���������P���ڸõ�ɵĵ糡���������˶�ʱ��ǡ���ܾ��������ε�������������a��b��c����ͼ��ʾ��������
������Q�̶��������ε�һ�������ϣ���������P���ڸõ�ɵĵ糡���������˶�ʱ��ǡ���ܾ��������ε�������������a��b��c����ͼ��ʾ��������| A�� | ����P������ | |
| B�� | a��b��c����ĵ��Ƹߵ�ϵ�Ǧ�a=��c����b | |
| C�� | ����P��a��b�����ܼ��٣���b��c���������� | |
| D�� | ����P��a��b��c����ļ��ٶȴ�С֮����2��1��2 |
19��һ���ػ��ĸ����ɾ�ֹ��ʼ�ȼ�����������Ϊm�������������ٶ�Ϊv1ʱ�����ػ��ﵽ�����P���Ժ����ػ����ָù��ʲ��䣬�����������ֱ���ﵽ����ٶ�v2Ϊֹ�������������У�����˵����ȷ���ǣ��������ٶ�Ϊg����������
| A�� | �������������Ϊmg | B�� | �������������Ϊ$\frac{P}{{v}_{2}}$ | ||
| C�� | �����ƽ���ٶȴ�СΪ$\frac{{v}_{1}+{v}_{2}}{2}$ | D�� | �����ȼ����˶��ļ��ٶ�$\frac{P}{m{v}_{1}}$-g |
9����������Բ���˶�������˵����ȷ���ǣ�������
| A�� | ����Բ���˶����������˶� | |
| B�� | ����Բ���˶���һ�ֱ�����˶� | |
| C�� | ����Բ���˶������崦��ƽ��״̬ | |
| D�� | ����Բ���˶��ļ��ٶ��Ǻ㶨����� |
13��һ����վ����̨�ϣ�����̨��Ե����ͬ������v0���ֱ������������ͬ������ֱ���ס���ֱ���ס�ˮƽ�׳������ƿ�����������Ƚ��������ʱ�Ķ�������˵��������ǣ�������
| A�� | ��������� | B�� | ��������� | C�� | ƽ������� | D�� | ����һ���� |
5����Ȼ����������ʾ����������
| A�� | ԭ�Ӳ��ǵ�һ�Ļ������� | B�� | ԭ�Ӻ˲��ǵ�һ�Ļ������� | ||
| C�� | ԭ���ڲ����ǿյ� | D�� | ԭ����һ�����ܼ� |
 ��ͼ��ʾ���ð����ͼ�е�Cλ���ɾ�ֹ��ʼ���£��ڵ���͵�D�������߸պñ����ϣ�С���ڴֲڵ�ˮƽ������D���������ȼ����˶�������СA����뾶R=0.3m����ֱ���õĹ⻬Բ����������������Բ��������ر�A�ף���֪���߳�L=2m����=60�㣬С������Ϊm=1kg��D����С��A��ˮƽ����s=2m��gȡ10m/s2������
��ͼ��ʾ���ð����ͼ�е�Cλ���ɾ�ֹ��ʼ���£��ڵ���͵�D�������߸պñ����ϣ�С���ڴֲڵ�ˮƽ������D���������ȼ����˶�������СA����뾶R=0.3m����ֱ���õĹ⻬Բ����������������Բ��������ر�A�ף���֪���߳�L=2m����=60�㣬С������Ϊm=1kg��D����С��A��ˮƽ����s=2m��gȡ10m/s2������