题目内容
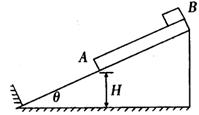
 固定在水平地面上表面光滑斜面倾角为θ.斜面底端固定一个与斜面垂直的挡板,一木板A被放在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示.木板和物块的质量均为m.相互间最大静摩擦力等于滑动摩擦力,动摩擦因数为μ(μ>tanθ),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块B始终不会与挡板发生碰撞.求:
固定在水平地面上表面光滑斜面倾角为θ.斜面底端固定一个与斜面垂直的挡板,一木板A被放在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示.木板和物块的质量均为m.相互间最大静摩擦力等于滑动摩擦力,动摩擦因数为μ(μ>tanθ),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块B始终不会与挡板发生碰撞.求:(1)木板A即将与挡板第一次碰撞前的速度为多大?
(2)木板A与挡板第一次碰撞后沿斜面上升的最大距离为多少?
(3)从释放木板到木板和物块都静止,木板和物块系统损失的机械能.
分析:(1)对木板向下运动到最低端时的过程,由机械能守恒定律即可求解速度;
(2)对A进行受力分析,求出加速度,根据匀减速直线运动位移速度公式即可求解;
(3)损失机械能等于阻力所做的功.
(2)对A进行受力分析,求出加速度,根据匀减速直线运动位移速度公式即可求解;
(3)损失机械能等于阻力所做的功.
解答:解:(1)对木板向下运动到最低端时的过程,由机械能守恒定律得:
×2m
=2mgH
解得
=
(2)上升的过程中对A进行受力分析得:
mgsinθ+f=ma①
f=μmgcosθ②
根据匀减速直线运动位移速度公式得:
2as1=v12③
由①②③得:s1=
=
(3)由机械能守恒mgH+mg(H+Lsinθ)=fL
损失机械能 E损=fL
解得 E损=
答:(1)木板A即将与挡板第一次碰撞前的速度为
;
(2)木板A与挡板第一次碰撞后沿斜面上升的最大距离为
;
(3)从释放木板到木板和物块都静止,木板和物块系统损失的机械能为
.
| 1 |
| 2 |
| v | 2 1 |
解得
| v | 1 |
| 2gH |
(2)上升的过程中对A进行受力分析得:
mgsinθ+f=ma①
f=μmgcosθ②
根据匀减速直线运动位移速度公式得:
2as1=v12③
由①②③得:s1=
| ||
| 2a |
| H |
| sinθ+μcosθ |
(3)由机械能守恒mgH+mg(H+Lsinθ)=fL
损失机械能 E损=fL
解得 E损=
| 2μmgHcosθ |
| μcosθ-sinθ |
答:(1)木板A即将与挡板第一次碰撞前的速度为
| 2gH |
(2)木板A与挡板第一次碰撞后沿斜面上升的最大距离为
| H |
| sinθ+μcosθ |
(3)从释放木板到木板和物块都静止,木板和物块系统损失的机械能为
| 2μmgHcosθ |
| μcosθ-sinθ |
点评:本题主要考查了机械能守恒定律、匀减速直线运动位移速度公式的应用,难度适中.

练习册系列答案
相关题目
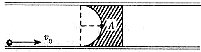
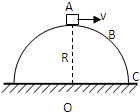 半径为R的光滑半圆柱固定在水平地面上,顶部有一小物块,如图所示,今给小物块一个初速度v0=
半径为R的光滑半圆柱固定在水平地面上,顶部有一小物块,如图所示,今给小物块一个初速度v0=| gR |
| A、沿圆面A、B、C运动 |
| B、先沿圆面AB运动,然后在空中作抛物体线运动 |
| C、立即离开圆柱表面做平抛运动 |
| D、立即离开圆柱表面作半径更大的圆周运动 |
 ”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“
”形的光滑长直导轨槽,槽口向上(图为俯视图).槽内放置一个木质滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,木质滑块的宽度为2R,比“ ”形槽的内侧宽度略小.现有一半径为r(r<<R)的金属小球以水平初速度v0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为5m,整个运动过程中无机械能损失.求:
”形槽的内侧宽度略小.现有一半径为r(r<<R)的金属小球以水平初速度v0冲向滑块,从滑块的一侧半圆形槽口边缘进入.已知金属小球的质量为m,木质滑块的质量为5m,整个运动过程中无机械能损失.求: