Question

【题目】如图所示为一竖直圆槽，AP、BP、CP为通过最低点P与水平面分别成30°、45°、60°角的三个粗糙斜面，与圆槽分别相交于A、B、C点．若一小物体由静止分别从A、B、C滑至P点所需的时间为t1，t2，t3，小物体与斜面间的摩擦因数相同，则（ ）

A. t1＞t2＞t3 B. t1=t2=t3 C. t1=t2＜t3 D. t1＜t2＜t3

Answer 1

【答案】A

【解析】设任一斜面的倾角为θ，圆槽直径为d．根据牛顿第二定律得到：物体的加速度 a==gsinθ-μgcosθ；斜面的长度为 x=dsinθ，则有：x= at2得 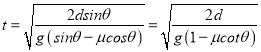，可见，斜面的倾角越大，cotθ越小，t越短．则有t1＞t2＞t3．故选A．

点睛: 本题的解题技巧是用相同的量表示物体运动和加速度和位移，再求出时间，分析时间关系，要知道该圆也称为等时圆．