��Ŀ����
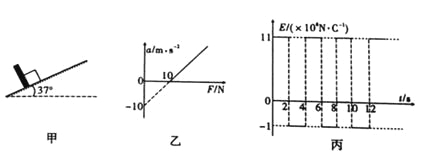
����Ŀ����ͼ��ʾ����б����=30���Ĺ⻬��б���������㹻������⻬ˮƽ���������ӣ�������Ⱦ�ΪL=1m��������Բ��ƣ���ǿ�ų�I���ֲ���ˮƽ���ƽ������������ˮƽ���ң���СB1=1T����ǿ�ų�II���ֲ�����б���ƽ������������ֱ����б���ƽ�����£���СB2=1T���ֽ���������Ϊm=0.2kg�������ΪR=0.5������ͬ�����ab��cd����ֱ�ڹ���ֱ�����ˮƽ����Ϻ���б����ϣ���ͬʱ�ɾ�ֹ�ͷţ�ȡg=10m/s2��
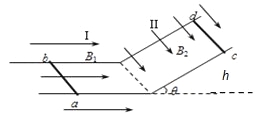
��1�������cd��б����»�������ٶȵĴ�С��
��2������֪�ӿ�ʼ�˶���cd���ﵽ����ٶȵĹ����У�ab�������Ľ�����Q=0.45J����ù�����ͨ��cd�������ĵ������
��3������֪cd����ʼ�˶�ʱ��ˮƽ����߶�h=10m��cd���ɾ�ֹ�ͷź�Ϊʹcd������Ӧ���������ôų����ĴŸ�Ӧǿ����ʱ��仯����cd����ʼ�˶���ʱ�̼�Ϊt=0����ʱ�ų����ĴŸ�Ӧǿ��ΪB0=1T������cd������б������»������ʱ���ڣ��ų����ĴŸ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵʽ��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
�������������������1����������ƽ��ͼ��cd�������»����������������ٶ���С�����ٶȼ�С����ʱ�ٶ��������![]() ����ʱcd�����ܺ���Ϊ�㣬�˺�cd�������»�����cd��������������ͼ��ʾ��
����ʱcd�����ܺ���Ϊ�㣬�˺�cd�������»�����cd��������������ͼ��ʾ��
�ص��췽����![]()
��Ӧ�綯��![]()
��Ӧ����![]()
������![]()
������ٶ�![]()
��2����cd���»�����Ϊxʱ��ab�������Ľ�����Q����ʱ��·���ܽ�����Ϊ2Q��
���������غ㶨�ɣ���![]()
����»�����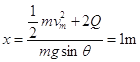
���ݷ����ڵ�Ÿ�Ӧ���ɣ���Ӧ�綯��ƽ��ֵ![]()
��Ӧ����ƽ��ֵ![]()
ͨ��cd�������ĵ����![]()
��3������·��û�и�Ӧ��������cd���ȼ����»������ٶ�Ϊ![]()
��ʼ״̬��·�д�ͨ��![]()
һ��ʱ��![]() ��cd���»�����
��cd���»�����![]()
��ʱ��·�д�ͨ��![]()
��·��û�и�Ӧ��������![]() ����
����![]()
���ϿɵôŸ�Ӧǿ��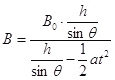
�������ݵã��Ÿ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵʽΪ![]()