Question

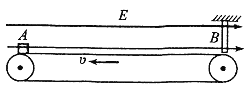
【题目】如图所示，A、B间相距L=6．25 m的水平传送带在电机带动下始终以v=3 m／s的速度向左匀速运动，传送带B端正上方固定一挡板，挡板与传送带无限接近但未接触，传送带所在空间有水平向右的匀强电场，场强E=l×l06 N/C。现将一质量m=2 kg．电荷量q=l×10-5C的带正电绝缘小滑块轻放在传送带上A端。若滑块每次与挡板碰后都以原速率反方向弹回，已知滑块与传送带间的动摩擦因数为μ=0．3，且滑块所受最大静摩擦力等于滑动摩擦力，取g=10 m／s2。求：

（1）滑块放上传送带后瞬间的加速度；

（2）滑块第一次反弹后能到达的距B端的最远距离；

（3）滑块做稳定的周期性运动后，电机相对于空载时增加的机械功率。

Answer 1

【答案】（1）a=2m/s2，方向水平向右；（2）3．25m；（3）18w

【解析】

试题分析：（l）滑块放上传送带后瞬间，受力如答图2所示

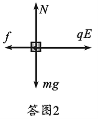
由牛顿第二定律有qE-mg=ma

代入数据解得a=2m/s2

方向水平向右

（2）设滑块第一次到达B点时速度为v1

由运动学规律有v12 =2aL

代入数据解得v1=5m/s

因v1＞v，故滑块与挡板碰后将向左做匀减速直线运动，其加速度方向向右，大小设为a1

由牛顿第二定律有qE+mg=ma1

代入数据得a1=8 m/s2

设滑块与档板碰后至速度减为v经历的时间为t1，发生的位移为x1

由运动学规律有v=v1-a1t1，x1=v1t1- a1t12

代入数据得t1=0．25s，x1=1m

此后．摩擦力反向（水平向左），加速度大小又变为a．滑块继续向左减速直到速度为零，

设这段过程发生的位移为x2

由运动学规律有x2=

代入数据得x2=2．25m

当速度为零时，滑块离B最远，最远距离xm=x1+x2

代入数据解得，xm=3．25m

（3）分析可知．滑块逐次回到B点的速度将递减,但只要回到B点的速度大于v．滑块反弹后总要经历两个减速过程直至速度为零，因此滑块再次向B点返回时发生的位移不会小于x2，回到B点的速度不会小于v'==3m/s

所以，只有当滑块回到B点的速度减小到v=3m/s后,才会做稳定的周期性往返运动。在周期性往返运动过程中，滑块给传送带施加的摩擦力方向始终向右

所以，滑块做稳定的周期性运动后，电机相对于空载时增加的功率为P=mgv

代人数据解得P=18w