题目内容
质量为m=1.0kg、带电量q=+2.5×10-4C的小滑块(可视为质点)放在质量为M=2.0kg的绝缘长木板的左端,木板放在光滑水平面上,滑块与木板之间的动摩擦因数为μ=0.2,木板长L=1.5m,开始时两者都处于静止状态,所在空间加有一个方向竖直向下强度为E=4.0×104N/C的匀强电场,如图所示,取g=10m/s2,试求: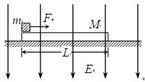
(1)用水平力F0拉小滑块,要使小滑块与木板以相同的速度一起运动,力F0应满足什么条件?
(2)用水平恒力F拉小滑块向木板的右端运动,在1.0s末使滑块从木板右端滑出,力F应为多大?
(3)按第(2)问的力F作用,在小滑块刚刚从木板右端滑出时,系统的内能增加了多少?(提示:设m与M之间最大静摩擦力与它们之间的滑动摩擦力大小相等,滑块在运动中带电量不变)
(1)F0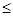 6.0N (2)9.0N (3)Q=6.0J
6.0N (2)9.0N (3)Q=6.0J
解析试题分析:(1)当拉力F0作用于滑块m上,木板在水平方向受力分析如图,其能够产生的最大加速度为: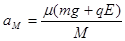 求得aM =2.0m/s2,根据题意为使滑块与木板共同运动,滑块最大加速度am≤aM
求得aM =2.0m/s2,根据题意为使滑块与木板共同运动,滑块最大加速度am≤aM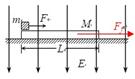
对于滑块受力分析则有: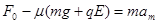
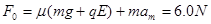
即为使滑块与木板之间无相对滑动,力F0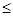 6.0N.
6.0N. 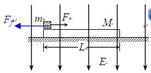
(2)设滑块相对于水平面的加速度为am,木板的加速度为aM,由运动学关系可知: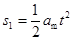 ,
, 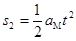 ,
,
滑动过程中木板的加速度aM =2.0m/s2 可得滑块运动的加速度am=5.0m/s2
对滑块:
(3)在将小滑块从木板右端拉出的过程中,系统的内能增加了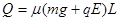 解得:Q=6.0J
解得:Q=6.0J
考点:受力分析、牛顿第二定律、运动学公式、系统内能公式
点评:此类题型考察根据受力分析从而可以写出牛顿第二定律公式,利用两物体运动的位移的相互关系,并结合运动学公式就能顺利得到物块加速度,最后利用系统内能公式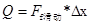 便可以求解出系统内能增加量。
便可以求解出系统内能增加量。

 如图所示,质量为m=1.0kg的小球从H=20m高处水平抛出的小球,除受重力外,还受到水平风力作用,假设受到的风力的大小恒定不变,g=10m/s2.问:
如图所示,质量为m=1.0kg的小球从H=20m高处水平抛出的小球,除受重力外,还受到水平风力作用,假设受到的风力的大小恒定不变,g=10m/s2.问:

 如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求:
如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求: