题目内容
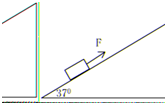 如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求:
如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求:(1)物体与斜面间的动摩擦因数.
(2)物体从绳断到再次返回斜面底端的时间.
分析:(1)对在拉力作用下上升的过程运用牛顿第二定律,求出物体与斜面间的动摩擦因数的大小.
(2)根据运动学公式求出向上匀加速直线运动的位移和末速度,结合牛顿第二定律和运动学公式求出向上匀减速运动的加速度和位移的大小,从而得出向下匀加速直线运动的位移,结合牛顿第二定律求出向下匀加速直线运动的加速度,通过位移时间公式求出向下匀加速直线运动的时间,从而得出物体从绳断到再次返回斜面底端的时间.
(2)根据运动学公式求出向上匀加速直线运动的位移和末速度,结合牛顿第二定律和运动学公式求出向上匀减速运动的加速度和位移的大小,从而得出向下匀加速直线运动的位移,结合牛顿第二定律求出向下匀加速直线运动的加速度,通过位移时间公式求出向下匀加速直线运动的时间,从而得出物体从绳断到再次返回斜面底端的时间.
解答:解:(1)上升过程对物块写牛顿第二定律可得:
F-mgsinθ-μmgcosθ=ma
解得:μ=
=
=0.25
(2)在时间 t1内位移为s1,绳断时速度为v1
则:s1=
at2=
×2×16m=16m
v1=at=2×4m/s=8m/s.
绳断后加速度大小为a2,继续上滑至速度为零时位移为s2 用时为t2,则有:
mgsinθ+μmgcosθ=ma2
解得:a2=gsinθ+μgcosθ=10×0.6+0.25×10×0.8=8m/s2
t2=
=
s=1s
根据v12=2a2s2
解得:s2=
=
m=4m
返回时加速度为a3,用时为t3,根据牛顿第二定律得:
mgsinθ-μmgcosθ=ma3
解得:a3=gsinθ-μgcosθ=10×0.6-0.25×10×0.8=4m/s2
根据s1+s2=
a3t32
代入数据解:得t3=
=
s
所以从绳断到再次返回斜面底端的时间为:
t=t2+t3=(
+1)s≈4.2s
答:(1)物体与斜面间的动摩擦因数为0.25.
(2)物体从绳断到再次返回斜面底端的时间为4.2s.
F-mgsinθ-μmgcosθ=ma
解得:μ=
| F-mgsinθ-ma |
| mgcosθ |
| 10-10×0.6-1×2 |
| 10×0.8 |
(2)在时间 t1内位移为s1,绳断时速度为v1
则:s1=
| 1 |
| 2 |
| 1 |
| 2 |
v1=at=2×4m/s=8m/s.
绳断后加速度大小为a2,继续上滑至速度为零时位移为s2 用时为t2,则有:
mgsinθ+μmgcosθ=ma2
解得:a2=gsinθ+μgcosθ=10×0.6+0.25×10×0.8=8m/s2
t2=
| v1 |
| a2 |
| 8 |
| 8 |
根据v12=2a2s2
解得:s2=
| v12 |
| 2a2 |
| 64 |
| 2×8 |
返回时加速度为a3,用时为t3,根据牛顿第二定律得:
mgsinθ-μmgcosθ=ma3
解得:a3=gsinθ-μgcosθ=10×0.6-0.25×10×0.8=4m/s2
根据s1+s2=
| 1 |
| 2 |
代入数据解:得t3=
|
| 10 |
所以从绳断到再次返回斜面底端的时间为:
t=t2+t3=(
| 10 |
答:(1)物体与斜面间的动摩擦因数为0.25.
(2)物体从绳断到再次返回斜面底端的时间为4.2s.
点评:解决本题的关键理清物体在整个过程中的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
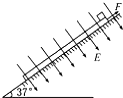 如图所示,长L=1.2m、质量M=3kg的木板放在倾角为37°的光滑斜面上,质量m=1kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8N.取g=10m/s2,斜面足够长.设图示位置木板和物块的速度均为零.求:
如图所示,长L=1.2m、质量M=3kg的木板放在倾角为37°的光滑斜面上,质量m=1kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8N.取g=10m/s2,斜面足够长.设图示位置木板和物块的速度均为零.求: 如图所示,长L=1.2m、质量M=3kg的木板放在倾角为37°的光滑斜面上,质量m=1kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8N.取g=10m/s2,斜面足够长.设图示位置木板和物块的速度均为零.试求:
如图所示,长L=1.2m、质量M=3kg的木板放在倾角为37°的光滑斜面上,质量m=1kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8N.取g=10m/s2,斜面足够长.设图示位置木板和物块的速度均为零.试求: 如图所示,足够长的光滑斜面的倾角为37°,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,且mA=3mB.开始时A物体离地高为h=0.5m,物体B恰在斜面底端,从图示位置由静止开始释放A物体,(取g=10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示,足够长的光滑斜面的倾角为37°,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,且mA=3mB.开始时A物体离地高为h=0.5m,物体B恰在斜面底端,从图示位置由静止开始释放A物体,(取g=10m/s2,sin37°=0.6,cos37°=0.8).求: