题目内容
一质点从地面开始竖直上抛，不计空气阻力，它上升了12m的A点时，速度减为初速度的一半，求
（1）质点的初速度的大小
（2）质点两次经过A点的时间间隔？（取g=10m/s2）
（1）质点的初速度的大小
（2）质点两次经过A点的时间间隔？（取g=10m/s2）
分析：竖直上抛运动是初速度向上，只在重力作用下的运动，加速度为g，上升和下落过程具有对称性，设出物体运动的初速度，根据匀减速直线运动位移速度公式可求得初速度大小，根据速度时间公式求出从A点上升的时间，根据对称性可知再次经过A点的时间从A点上升到最高点的两倍．
解答：解：（1）设初速度为v0，则
v02-(
)2=2gh
代入数据解得：v0=8
m/s
（2）从A点上升的时间t1=
=
s
根据对称性可知：质点两次经过A点的时间间隔t=2t1=
s
答：（1）质点的初速度的大小为8
m/s；
（2）质点两次经过A点的时间间隔为
s．
v02-(
| v0 |
| 2 |
代入数据解得：v0=8
| 5 |
（2）从A点上升的时间t1=
| ||
| g |
2
| ||
| 5 |
根据对称性可知：质点两次经过A点的时间间隔t=2t1=
4
| ||
| 5 |
答：（1）质点的初速度的大小为8
| 5 |
（2）质点两次经过A点的时间间隔为
4
| ||
| 5 |
点评：该题主要考查了竖直上抛运动的基本规律，要求同学们知道，竖直上抛运动是初速度向上，只在重力作用下的运动，加速度为g，上升和下落过程具有对称性，难度不大，属于基础题．
练习册系列答案
灵星计算小达人系列答案
相关题目
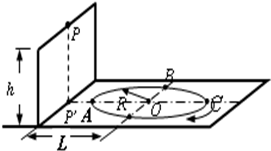水平地面上有一个半径为R的圆形轨道，竖直平面上边中点P离地面高为h，P正下方一点P′位于COA连线上且与轨道圆心O的距离为L（L＞R），如图所示．现从P点水平抛出质量为m的小球，（小球与小车均视为质点，空气阻力不计）．求：