题目内容
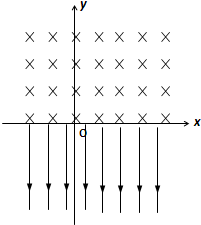在xoy平面内，x轴的上方有匀强磁场，磁感应强度为B，方向如图所示，x轴的下方有匀强电场，电场强度为E，方向与y轴的正方向相反．今有电量为-q、质量为m的粒子（不计重力），从坐标原点沿y轴的正方向射出，射出以后，第三次到达x轴时（出发点O不包括在这三次内），它与O点的距离为L，问：（1）粒子射出时的速度多大？
（2）粒子运动的总路程为多少？
分析：（1）粒子在磁场中做圆周运动，转动半周后到达电场先减速再反向加速，以大小不变的速度反向进入磁场，再次偏转；由题意可知半径大小，由洛仑兹力充当向心力可求得粒子的速度；
（2）粒子的总路程包括电场中的路程和磁场中的路程，求出两场中的过程即可求出总路程．
（2）粒子的总路程包括电场中的路程和磁场中的路程，求出两场中的过程即可求出总路程．
解答：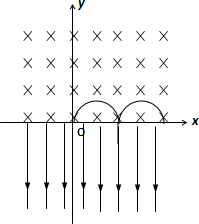
解：（1）由题意知第3次经过x轴的运动如图所示：L=4R
设粒子初速度为v，则有：qvB=m
可得：v=
；
（2）设粒子进入电场作减速运动的最大路程为L′，加速度为a，则有：
v2=2aL′
qE=ma
则电场中的路程：L′=
粒子运动的总路程：s=2πR+2L'=
+
答：（1）粒子射出的速度为
；
（2）粒子的总路程为
+
．
解：（1）由题意知第3次经过x轴的运动如图所示：L=4R设粒子初速度为v，则有：qvB=m
| v2 |
| R |
可得：v=
| qBL |
| 4m |
（2）设粒子进入电场作减速运动的最大路程为L′，加速度为a，则有：
v2=2aL′
qE=ma
则电场中的路程：L′=
| qB2L2 |
| 16mE |
粒子运动的总路程：s=2πR+2L'=
| πL |
| 2 |
| qB2L2 |
| 16mE |
答：（1）粒子射出的速度为
| qBL |
| 4m |
（2）粒子的总路程为
| πL |
| 2 |
| qB2L2 |
| 16mE |
点评：带电粒子在磁场中的题目关键在于明确圆心和半径，注意要根据题意找出合理的运动过程，从而得出正确的结论．
练习册系列答案
相关题目
（2008?韶关一模）如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P1（-a，0）点以相同的速率vo在xOy平面内朝x轴上方的各个方向射出（即0＜θ≤π），不计重力及粒子间的相互作用，且已知a足够大．
如图所示，在O-XYZ的空间中，分布着以XOZ平面为边界的匀强磁场，XOZ平面的上方磁场的磁感应强度为B，XOZ平面下方磁场的磁感应强度为B，两磁场方向均沿Z轴正方向，且B2=3Bl．今有一带正电的粒子在XOY平面内自X轴上的P点出发，以初速度V0进入磁场Bl中，V0的方向与X轴正方向成30°角，大小为6.28m/s．（粒子的重力不计，π的值取3.14）