题目内容
如图所示，在O-XYZ的空间中，分布着以XOZ平面为边界的匀强磁场，XOZ平面的上方磁场的磁感应强度为B，XOZ平面下方磁场的磁感应强度为B，两磁场方向均沿Z轴正方向，且B2=3Bl．今有一带正电的粒子在XOY平面内自X轴上的P点出发，以初速度V0进入磁场Bl中，V0的方向与X轴正方向成30°角，大小为6.28m/s．（粒子的重力不计，π的值取3.14）（1）画出粒子自P点出发后的运动轨迹示意图（至少画出二次经过X轴的情况）；
（2）求出粒子自P点出发后到第四次经过X轴的时间内平均速度的大小．
分析：根据半径与速度垂直确定，然后根据两磁场之比求出半径之比，画出轨迹；
根据牛顿第二定律推导出半径公式，根据半径与周期关系公式推导出周期公式，结合轨迹算出粒子前进的位移，平均速度等于位移除以时间．
根据牛顿第二定律推导出半径公式，根据半径与周期关系公式推导出周期公式，结合轨迹算出粒子前进的位移，平均速度等于位移除以时间．
解答：解：设粒子运动的轨迹半径分别为r1、r2；周期分别为T1、T2
（1）粒子在磁场B1中轨迹长度是以r1为半径的圆周长的
，粒子在B2磁场中的轨迹长度是以r2为半径的圆周长的
，又r2=
；故轨迹如图所示．
（2）根据牛顿第二定律：qv0B=m
①
又：T1=
②
由①②得：r1=
T1=
同理可得：r2=
T2=
粒子前进的轨迹如上图，可以看出粒子前进的位移S=PP4=r1+r2=
粒子前进的时间t=2（
+
）=
粒子运行的平均速度
=
=
=1.5m/s
答：（1）如图．
（2）粒子自P点出发后到第四次经过X轴的时间内平均速度的大小1.5m/s．
（1）粒子在磁场B1中轨迹长度是以r1为半径的圆周长的
| 1 |
| 6 |
| 5 |
| 6 |
| r1 |
| 3 |
（2）根据牛顿第二定律：qv0B=m
| v02 |
| r1 |
又：T1=
| 2πr1 |
| v0 |
由①②得：r1=
| mv0 |
| qB1 |
T1=
| 2πm |
| qB1 |
同理可得：r2=
| r1 |
| 3 |
T2=
| T1 |
| 3 |
粒子前进的轨迹如上图，可以看出粒子前进的位移S=PP4=r1+r2=
| 4mv0 |
| 3qB1 |
粒子前进的时间t=2（
| T1 |
| 6 |
| 5T2 |
| 6 |
| 16πm |
| 9qB1 |
粒子运行的平均速度
. |
| v |
| S |
| T |
| 3v0 |
| 4π |
答：（1）如图．
（2）粒子自P点出发后到第四次经过X轴的时间内平均速度的大小1.5m/s．
点评：带电粒子在磁场中运动的题目解题步骤为：定圆心、画轨迹、求半径．要掌握左手定则，熟练运用牛顿第二定律研究半径．
练习册系列答案
相关题目
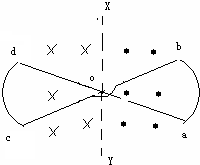
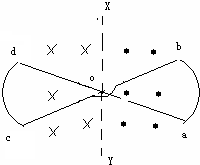如图所示，在直线XY的右边磁场方向垂直纸面向外，左边磁场方向垂直纸面向里，两边磁场强度大小相等，有半径一定，顶角为θ的两个扇形导体框交叉在一起组成框架abcd，在该磁场中以XY上的一点o为中心以恒定角速度按顺时针方向在垂直于磁感线的平面内旋转半周，则在框架内（ ）
的两个扇形导体框交叉在一起组成框架abcd，在该磁场中以XY上的一点o为中心以恒定角速度按顺时针方向在垂直于磁感线的平面内旋转半周，则在框架内： （ ）