Question

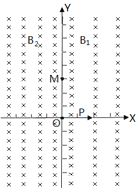
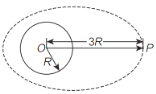
【题目】如图所示，MPQO为有界的竖直向下的匀强电场（边界上有电场），电场强度E=。ACB为光滑竖直固定的半圆形轨道，轨道半径为R，A,B为圆水平直径的两个端点，AC为圆弧。一个质量为m，电荷量为﹣q（q>0）的带电小球，从A点正上方高为H=R处由静止释放，并从A点沿切线进入半圆轨道，不计空气阻力及一切能量损失，关于带电小球的受力及运动情况，下列说法正确的是（　 　）

A. 小球在AC部分运动时，加速度不变

B. 适当增大E，小球沿轨道到达C点的速度可能为零

C. 小球到达C点时对轨道压力大小为2mg

D. 若，要使小球沿轨道运动到C，则应将H至少调整为

Answer 1

【答案】CD

【解析】

因mg=qE，则电场力与重力的合力为零，则小球在AC部分做匀速圆周运动，加速度大小不变，方向始终指向圆心。故A错误。适当增大E，即小球所受的电场力大于重力，电场力和重力的合力向上，则在最低点C的最小速度满足Eq-mg=m，即在最低点的速度不可能为零，故B错误。小球进入半圆轨道，电场力和重力平衡，小球做匀速圆周运动，根据动能定理知，mgH=mvA2-0，解得：vA=。根据牛顿第二定律得：N=m=2mg，则小球到达C点时对轨道的压力为2mg。故C正确。若E=，在最低点轨道的作用力为零，根据牛顿第二定律得，qE-mg=m，解得：vC=，根据动能定理得：mg（H+R）-qER=mvC2-0，解得：H=R．所以H至少为R．故D正确。故选CD。