Question

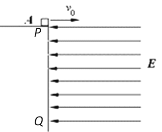
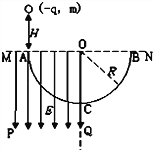
【题目】如图所示，光滑水平面内有方向垂直纸面向里的匀强磁场，X＞0一侧磁感应强度的大小为B1，X＜0一侧磁感应强度的大小为B2，且B1∶B2＝3∶4。t＝0时刻坐标原点O处，一个静止的中性粒子裂变为两个带电粒子P和Q，质量分别为m1和m2，已知粒子P带正电，分裂时速度沿X轴正方向，在磁场B1中做圆周运动的半径为R。在以后的运动过程中忽略两粒子之间的相互作用。求：

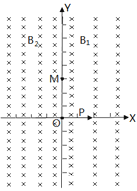
（1）粒子Q在磁场B1中运动半径r。

（2）若两粒子在两磁场分界线上M点相遇，M点离O点的距离为R，则m1∶m2是多少？

Answer 1

【答案】(1) r＝3R/4 (2) m1∶m2＝1∶7

【解析】

(1)中性粒子分裂成两个带电粒子时，两粒子所带电电量相等，设为q，电性相反。设两粒子P、Q分裂时速度的大小分别为V1、V2，且方向相反。由动量守恒定律得：

m1 V1 ＝m2V2

对两粒子P、Q，由牛顿第二定律知：

B1q V1＝m1 V12/R

B2q V2＝m2V22/r

联立解得：r＝3R/4；

(2) 带电粒子在匀强磁场中运动的周期T＝2πm/Bq

故两粒子P、Q运动的周期分别为T1、T2

T1＝πm1/qB1＋πm1/B2q

T2＝πm2/qB2＋πm2/B1q

由于OM=

由此知粒子Q恰好运动了半个周期。即t＝πm2/qB2

在时间t内粒子P要经过M点，必须要在磁场中运动3个周期，如图所示

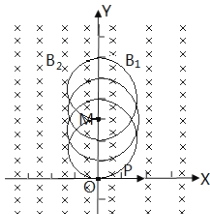
即t＝3T1 ＝3πm1/qB1＋3πm1/B2q

联立解得：m1∶m2＝1∶ 7 。