题目内容
【题目】一根粗细均匀的金属导线阻值为R,两端加上恒定电压U时,通过金属导线的电流强度为I,金属导线中自由电子定向移动的平均速率为v,若将金属导线均匀拉长,使其长度变为原来的2倍,仍给它两端加上恒定电压U,则下列说法中正确的是( )
A. 此时金属导线的阻值为4R
B. 此时通过金属导线的电流为 ![]()
C. 此时自由电子定向移动的平均速率为![]()
D. 此时自由电子定向移动的平均速率为 ![]()
【答案】ABC
【解析】
将金属导线均匀拉长,使其长度变为原来的2倍,横截面积变为原来的![]() 倍,,根据电阻定律
倍,,根据电阻定律![]() 分析电阻的变化,由欧姆定律分析电流的变化.由电流的微观表达式I=nevS分析平均速率v的变化。
分析电阻的变化,由欧姆定律分析电流的变化.由电流的微观表达式I=nevS分析平均速率v的变化。
A项:将金属导线均匀拉长,使其长度变为原来的2倍,横截面积变为原来的![]() 倍,根据电阻定律
倍,根据电阻定律![]() 分析得到,电阻变为原来的4倍,故A正确;
分析得到,电阻变为原来的4倍,故A正确;
B项:根据欧姆定律![]() 可知,电流I变为原来的
可知,电流I变为原来的![]() ,即为
,即为![]() ,故B正确;
,故B正确;
C、D项:电流的微观表达式I=nevS,其中n、e不变,电流I为原来的![]() ,横截面积S变为原来的
,横截面积S变为原来的![]() 倍,则自由电子定向移动的平均速率为
倍,则自由电子定向移动的平均速率为![]() ,故C正确,D错误。
,故C正确,D错误。
故应选ABC。

 名校课堂系列答案
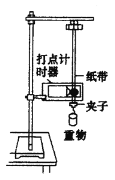
名校课堂系列答案【题目】如图甲所示,某组同学借用“探究a与F、m之间的定量关系”的相关实验思想、原理及操作,进行“研究合外力做功和动能变化的关系”的实验:
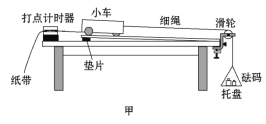
①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做____运动。
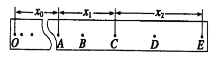
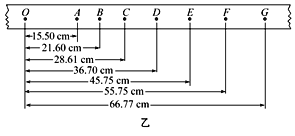
②连接细绳及托盘,放入砝码,通过实验得到图乙所示的纸带。纸带上O为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G。实验时小车所受拉力为0.2N,小车的质量为0.2kg。请计算小车所受合外力做的功W和小车动能的变化ΔEk,补填表中空格里_____________ 、_____________ (结果保留至小数点后第四位)。
O—B | O—C | O—D | O—E | O—F | |
W/J | 0.0432 | 0.0572 | 0.0734 | 0.0915 | |
ΔEk/J | 0.0430 | 0.0570 | 0.0734 | 0.0907 |
分析上述数据可知:_______________________。