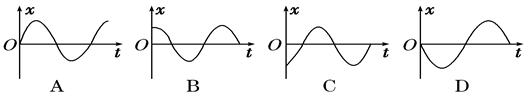题目内容
如图所示,两个大小可忽略的质量相等的弹性小球A和B分别挂在L1=1m,L2=0.25m的细线上,两球重心等高且互相接触.现将A球向左拉离平衡位置很小的角度后由静止开始释放,已知当A与B相碰时发生速度交换,即碰后A球速度为零,B球速度等于A球碰前的速度,当B与A相碰时遵循相同的规律,且碰撞时间极短忽略不计.A、B两球的运动可视为简谐运动.求从释放小球A开始到两球发生第3次碰撞的时间t.(取π2≈g)


2s
试题分析:两质量相等的弹性小球做弹性正碰时,两球速度交换。
由单摆周期公式有 TA=2π="2s" ,TB=2π=1s
从释放小球A到第1次相碰经历时间 t1= =0.5s
从小球B摆起到第2次相碰经历时间 t2= =0.5s
从小球A摆起到第3次相碰经历时间 t3= =1s
所以从释放小球A到A、B第3次碰撞,共需时间 t=t1+t2+t3=2s
点评:本题虽然没有使用动量守恒定律计算但是通过题意告诉了动量守恒的结论,通过单摆知识巧妙的结合在一起。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目


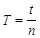 ;
;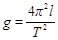 计算重力加速度
计算重力加速度 时,摆球具有负向最大速度,则单摆的振动图象是图中的 ( )
时,摆球具有负向最大速度,则单摆的振动图象是图中的 ( )