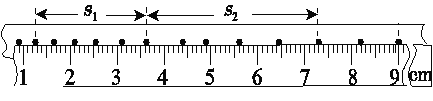题目内容
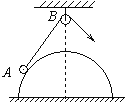
【题目】如图所示,固定在水平面上半径为R的光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮,如图所示![]() 已知小定滑轮到半球顶点的高度为H,绳子的长度为L。今缓慢拉绳使小球从A点滑向半球顶点
已知小定滑轮到半球顶点的高度为H,绳子的长度为L。今缓慢拉绳使小球从A点滑向半球顶点![]() 未到顶点
未到顶点![]() ,则此过程中,半球对小球的支持力大小N及细绳的拉力T大小的变化情况是
,则此过程中,半球对小球的支持力大小N及细绳的拉力T大小的变化情况是
A. N不变,T变小 B. N不变,T变大
C. N变小,T变大 D. N变大,T变小
【答案】A
【解析】
小球在绳的拉力作用下缓慢运动的过程中可视为小球受力平衡,对小球进行受力分析,根据平衡可以求出小球拉力和支持力大小的变化;
在小球被拉升的过程中对小球进行受力分析,小球受重力、半球面对小球的弹力和绳对小球的拉力,小球在三个力作用下缓慢滑向半球顶点,可视为小球在运动过程中受力平衡,即小球受重力、支持力和绳拉力的合力为0,作出小球的受力示意图如图所示: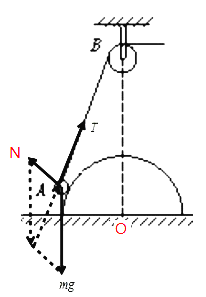
因为小球所受合力为零,故小球所受重力mg、半球对小球的弹力N和绳对小球的拉力T可以构成一个闭合的矢量三角形,如图可知,三个力构成的三角形与图中由绳AB、顶点高度BO及半球半径AO构成的三角形ABO始终相似,故有:![]() ,由于小球在上拉的过程中,BO和AO的长度不变,AB减小,在力中由于重力不变,所以根据相似比可以得出:小球的拉力T变小,半球对小球的支持力N不变,故选项A正确,选项BCD错误。
,由于小球在上拉的过程中,BO和AO的长度不变,AB减小,在力中由于重力不变,所以根据相似比可以得出:小球的拉力T变小,半球对小球的支持力N不变,故选项A正确,选项BCD错误。

 口算能手系列答案
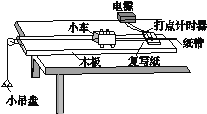
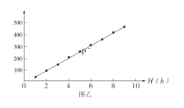
口算能手系列答案【题目】某同学利用如图甲所示的装置验证动能定理。固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺放好木板、白纸、复写纸。将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x。改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:
高度 H(h为单位长度) | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
水平位移 x/cm | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |
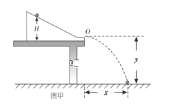
(1)已知斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ,斜槽底端离地的高度为y,不计小球与水平槽之间的摩擦,小球从斜槽上滑下的过程中,动能定理若成立应满足的关系式是______________________;
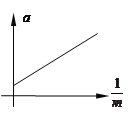
(2)以H为横坐标,以__________为纵坐标,在坐标纸上描点作图,如图乙所示;由第(1)、(2)问,可以得出结论:在实验误差允许的范围内,小球运动到斜槽底端的过程中,合外力对小球所做的功等于动能变化量。
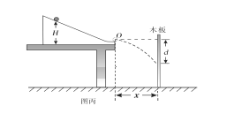
(3)受该实验方案的启发,某同学改用图丙的装置实验。他将木板竖直放置在斜槽末端的前方某一位置固定,仍将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并测量小球击中木板时平抛下落的高度d,他以H为横坐标,以________为纵坐标,描点作图,使之仍为一条倾斜的直线,也达到了同样的目的。