题目内容
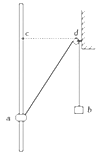
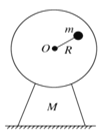
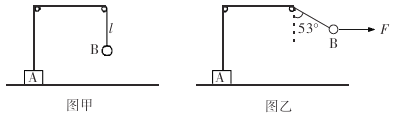
【题目】如图甲所示，物块A与质量为m的小球B通过不可伸长的轻质细绳跨过两等高定滑轮连接。物块A置于左侧滑轮正下方的表面水平的压力传感装置上，小球与右侧滑轮的距离为l0开始时物块和小球均静止，将此时传感装置的示数记为N1。现给小球施加水平力F,将小球缓慢拉起至细绳与竖直方向成53°角，如图乙所示，此时传感装置的示数记为N2，已知N1:N2=9:7；再将小球由静止释放，当小球B运动至最低位置时，传感装置的示数与刚释放时恰好相同，不计滑轮的大小和摩擦，重力加速度的大小为g。求：
（1）物块A的质量M与小球B的质量m之比：
（2）从释放到运动至最低位置的过程中，小球克服阻力所做的功；
（3）若小球释放后忽略阻力的影响，小球运动到最低点时传感装置的示数N3
【答案】（1）4:1（2）
（3）2．2mg
【解析】
试题分析：（1）初始时：N1=Mg-mg
F作用时，在530时，绳的拉力：
此时 N2=Mg-T1
又：N1：N2=9：7
解得：M:m=4:1
（2）从释放到最低点，由动能定理：
在最低点：
解得：
（3）无空气阻力时，由动能定理：
在最低点：
解得：
传感器示数：N3=Mg-T2=2．2mg
练习册系列答案
备战中考寒假系列答案
相关题目
